任何无限循环小数都可以化作分数的形式,例如:
如果规定:0.111……记作![]() ,0.234234234……记作
,0.234234234……记作![]() ,0.2343434……记作
,0.2343434……记作![]()
求证:![]()
证明:设0.111111……=![]() ,则10×0.111111……=
,则10×0.111111……=![]()
即1.11111……=![]() ,1+0.1111……=
,1+0.1111……=![]()
∴![]() ,得
,得![]() ,∴
,∴![]() ,即
,即![]()
(1)试比较0.9999……与1的大小,并说明理由
(2)把以下小数化作分数![]() = ,
= ,![]() = ,
= ,![]() = 。
= 。
答案
解:(1)设0.999999……=![]() ,则10×0.999999……=
,则10×0.999999……=![]()
即9.999999……=![]() ,9+0.999999……=
,9+0.999999……=![]()
∴![]() ,得
,得![]()
∴![]() ,即
,即![]() (或
(或![]() )
)
(2)![]()
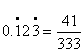
![]()