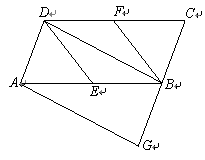
如图，已知正方形ABCD，点E是BC上一点，
以AE为边作正方形AEFG。
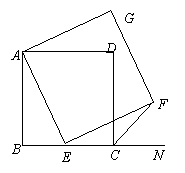（1）连结GD，求证△ADG≌△ABE；
（2）连结FC，求证∠FCN=45°；
（3）请问在AB边上是否存在一点Q，
使得四边形DQEF是平行四边形？
若存在，请证明；若不存在，请说明理由。
答案
1）如图，连接DG
∵四边形ABCD和四边形AEFG是正方形
∴DA=BA，EA=GA，∠BAD=∠EAG=90°
∴∠DAG=∠BAE
∴△ADG≌△ABE；
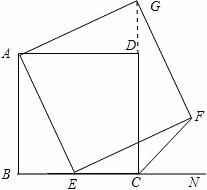（2）过F作BN的垂线，设垂足为H
∵∠BAE+∠AEB=90°，∠FEH+∠AEB=90°
∴∠BAE=∠HEF
∵AE=EF
∴△ABE≌△EHF
∴AB=EH，BE=FH
∴AB=BC=EH
∴BE+EC=EC+CH
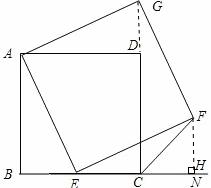∴CH=BE=FH
∴∠FCN=45°；
（3）在AB上取AQ=BE，连接QD
∵AB=AD
∴△DAQ≌△ABE
∵△ABE≌△EHF
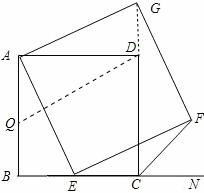∴△DAQ≌△ABE≌△ADG
∴∠GAD=∠ADQ
∴AG、QD平行且相等
又∵AG、EF平行且相等
∴QD、EF平行且相等
∴四边形DQEF是平行四边形
∴在AB边上存在一点Q，使得四边形DQEF
是平行四边形．
