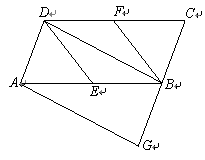
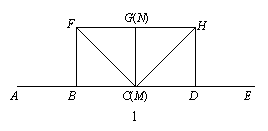
在图1至图3中,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和CDHN都是正方形.AE的中点是M.
(1)如图1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,求证:FM = MH,FM⊥MH;
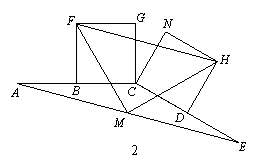
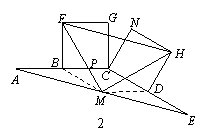
(2)将图1中的CE绕点C顺时针旋转一个锐角,得到图23-2,求证:△FMH是等腰直角三角形;
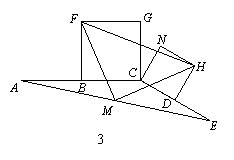
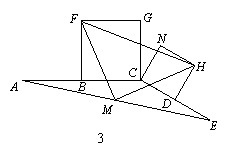
(3)将图23-2中的CE缩短到图23-3的情况,△FMH还是等腰直角三角形吗?(直接写出结论,不必证明).
 |
 |
 |
答案
(1)证明:∵四边形BCGF和CDHN都是正方形,
又∵点N与点G重合,点M与点C重合,
∴FB = BM = MG = MD = DH,∠FBM =∠MDH = 90°.
∴△FBM ≌ △MDH.∴FM = MH
∵∠FMB =∠DMH = 45°,∴∠FMH = 90°.∴FM⊥HM
(2)证明:连接MB、MD,如图23-2,设FM与AC交于点P.
∵B、D、M分别是AC、CE、AE的中点,
∴MD∥BC,且MD = BC = BF;MB∥CD,
且MB=CD=DH
∴四边形BCDM是平行四边形.∴ ∠CBM =∠CDM
又∵∠FBP =∠HDC,∴∠FBM =∠MDH.∴△FBM ≌ △MDH
∴FM = MH, 且∠MFB =∠HMD
又∵MD∥BC,∴∠FMD=∠APM,
∴∠FMH =∠FMD-∠HMD =∠APM-∠MFB =∠FBP = 90°.
∴△FMH是等腰直角三角形
(3)解:△FMH是等腰直角三角形…
 |
 |
 |