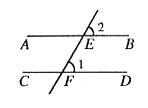
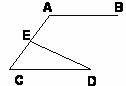
如图,下列推理及所注明的理由都正确的是( )
|
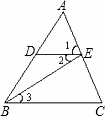
| A. | 因为DE∥BC,所以∠1=∠C(同位角相等,两直线平行) |
|
| B. | 因为∠2=∠3,所以DE∥BC(两直线平行,内错角相等) |
|
| C. | 因为DE∥BC,所以∠2=∠3(两直线平行,内错角相等) |
|
| D. | 因为∠1=∠C,所以DE∥BC(两直线平行,同位角相等) |
答案
考点:
平行线的判定与性质.
分析:
A的理由应是两直线平行,同位角相等;
B的理由应是内错角相等,两直线平行;
D的理由应是同位角相等,两直线平行;
所以正确的是C.
解答:
解:A、因为DE∥BC,所以∠1=∠C(两直线平行,同位角相等);
B、因为∠2=∠3,所以DE∥BC(内错角相等,两直线平行);
C、因为DE∥BC,所以∠2=∠3(两直线平行,内错角相等);
D、因为∠1=∠C,所以DE∥BC(同位角相等,两直线平行).
故选C.
点评:
正确区分平行线的性质和判定是解决此类问题的关键.