下列四个命题：①一组对边平行且一组对角相等的四边形是平行四边形；②对
角线互相垂直且相等的四边形是正方形；③顺次连结矩形四边中点得到的四边形是菱形；④正五边形既是
轴对称图形又是中心对称图形．其中真命题共有【 】
A．1个 
B．2个 C．3个 D．4个
答案
B。
【考点】真假命题，平行四边形的判定，正方形的判定，菱形的判定，轴对称图形和中心对称图形。
【分析】根据平行四边形的判定，正方形的判定，菱形的判定和轴对称图形、中心对称图形的概念逐一作出判断：
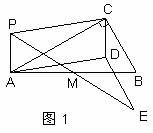
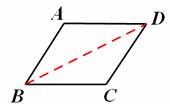
①如图，四边形ABCD中，AD∥BC，∠ADC=∠ABC，
连接BD，则
∵AD∥BC，∴∠ADB=∠DBC（两直线平行，内错角相等）。
又∵∠ADC=∠ABC，∴∠BDC=∠ABD（等量减等量，差相等）。
∴AB∥DC（内错角相等，两直线平行）。
∴四边形ABCD是平行四边形（平行四边形定义）。因此命题①正确。
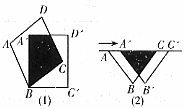
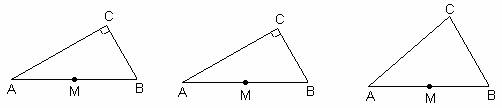
②举反例说明，如图，铮形对角线互相垂直且相等。因此命题②错误。
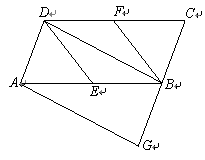
③如图，矩形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点，
连接AC，BD。
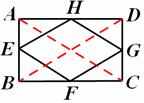∵E、F、G、H分别是AB、BC、CD、DA的中点，
∴EF=
AC，HG=AC，EF=BD，FG=BD（三角形中位线定理）。
又∵矩形ABCD，∴AC=BD（矩形的对角线相等）。
∴EF=HG=EF=FG（等量代换）。
∴四边形EFGH是菱形（四边相等的辊边形是菱形）。因此命题③正确。
④根据轴对称图形和中心对称图形的概念，正五边形是轴对称图形，不是中心对称图形。因此命题④错误。
综上所述，正确的命题即真命题有①③。故选B。
