下列各组图形中,能将其中一个图形经过平移变换得到另一个图形的是( )
A.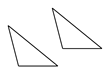 B.
B.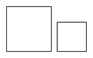 C.
C.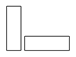 D.
D.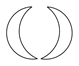
A
【分析】
根据平移的性质,再结合图形逐项排查即可解答.
【详解】
解:在选项中的各组图形中,只有选项A中的图形是一个图形经过平移能得到另一个图形.
故答案为A.
【点睛】
本题主要考查了平移的性质,掌握平移只改变图形的位置、不改变图形的大小且平移前后对应边平行是解答本题的关键.
中国国家航天局2020年4月24日在“中国航天日”之际宣布,将中国行星探测任务命名为“天问”,将中国首次火星探测任务命名为“天问一号”.火星具有与地球十分相近的环境,与地球最近的时候距离约5500万千米,将5500用科学记数法表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
B
【分析】
根据科学记数法的表示形式对数值进行表示即可.
【详解】
解:5500=5.5×103,
故选:B.
【点睛】
本题考查了科学记数法,掌握科学记数法的形式是解题关键.
如图是某个几何体的平面展开图,该几何体是( )
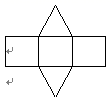
A.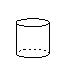 B.
B.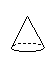 C.
C.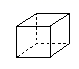 D.
D.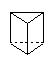
D
【分析】
由平面图形的折叠及三棱柱的展开图的特征作答.
【详解】
由侧面是3个矩形,上下为2个三角形,可得该几何体为三棱柱
故选:D.
【点睛】
此题主要考查了几何体的展开图,熟记常见立体图形的平面展开图的特征是解决此类问题的关键.
下列运算正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
A
【解析】
根据同底数幂乘除法的运算法则,合并同类项法则,幂的乘方与积的乘方法则即可求解;
【详解】
解:![]() ,A准确;
,A准确;
![]() ,B错误;
,B错误;
![]() ,C错误;
,C错误;
![]() ,D错误;
,D错误;
故选:A.
【点睛】
本题考查实数和整式的运算;熟练掌握同底数幂乘除法的运算法则,合并同类项法则,幂的乘方与积的乘方法则是解题的关键.
如图,实数a,b在数轴上的对应点的位置如图所示,则正确的结论是( )
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
C
【分析】
观察数轴得到实数a,b,c的取值范围,根据实数的运算法则进行判断即可.
【详解】
∵−3<a<−2,∴2<|a|<3,故A选项错误;
∵1<b<2,∴﹣2<﹣b<﹣1,故B选项正确;
∵a<0,b>0,|a|>|b|,∴a<﹣b,故C选项正确;a+b<0,故D选项错误.
故选C.
【点睛】
本题主要考查数轴、绝对值以及实数及其运算,学会观察数轴是解题的关键.
本卷还有51题,登录并加入会员即可免费使用哦~

该作品由: 用户苏晓木分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。