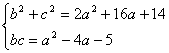2006人教版初中数学竞赛3094
初中
整体难度：中等
2009-03-15
题号
一
二
三
四
五
评分
一、计算题 (共7题)
添加该题型下试题
1.
已知
，
，
为互质的正整数（即，是正整数，且它们的最大公约数为1），且≤8，
．
（1） 试写出一个满足条件的x；
（2） 求所有满足条件的x．
难度：
知识点：一元一次不等式组
使用次数：161
【答案】
解：（1）
满足条件．
（2）因为
，
，为互质的正整数，且≤8，所以
， 即 
．
当a=1时，
，这样的正整数
不存在．
当a=2时，
，故=1，此时．
当a=3时，
，故=2，此时
．
当a=4时，
，与互质的正整数不存在．
当a=5时，
，故=3，此时
．
当a=6时，
，与互质的正整数不存在．
当a=7时，
，故=3，4，5此时
，
，
．
当a=8时，
，故=5，此时
所以，满足条件的所有分数为
，
，
，
，，，
2.
10个学生参加n个课外小组，每一个小组至多5个人，每两个学生至少参加某一个小组，任意两个课外小组，至少可以找到两个学生，他们都不在这两个课外小组中．求n的最小值．
难度：
知识点：数学竞赛
使用次数：87
【答案】
解：设10个学生为
，
，…，
，n个课外小组
，
，…，
．
首先，每个学生至少参加两个课外小组．否则，若有一个学生只参加一个课外小组，设这个学生为，由于每两个学生至少在某一个小组内出现过，所以其它9个学生都与他在同一组出现，于是这一组就有10个人了，矛盾．
若有一学生恰好参加两个课外小组，不妨设恰好参加，，由题设，对于这两组，至少有两个学生，他们没有参加这两组，于是他们与没有同过组，矛盾．
所以，每一个学生至少参加三个课外小组．于是n个课外小组，，…，的人数之和不小于3×10=30．
另一方面，每一课外小组的人数不超过5，所以n个课外小组，，…，的人数不超过5n， 故 5n≥30， 所以n≥6．
下面构造一个例子说明n=6是可以的．
，
，
，
，
，
．
容易验证，这样的6个课外小组满足题设条件．
所以，n的最小值为6．
3.
2006个都不等于119的正整数
，
，…，
排列成一行数，其中任意连续若干项之和都不等于119，求
…
的最小值.
难度：
知识点：实数单元测试
使用次数：282
【答案】
2×2006－33×2－1＝3945
“1，2，2，…，2（58个2），1”；
“1，2，2，…，2（58个2），1”； 33组
……
“1，2，2，…，2（58个2），1”；
“1，2，2，…，2（25个2）.
4.
如图，点P为⊙O外一点，过点P作⊙O的两条切线，切点分别为A，B. 过点A做PB的平行线，交⊙O于点C. 连结PC，交⊙O于点E；连结AE，并延长AE交PB于点K. 求证：
.
难度：
知识点：圆单元测试
使用次数：171
【答案】
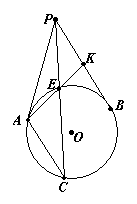
两次相似，再加上切割线定理
，
.
本卷还有15题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
20
总体难度：
中等
难度统计
难度系数
数量
占比
中等
19
95.0%
容易
1
5.0%
题型统计
大题类型
数量
占比
计算题
7
35.0%
填空题
5
25.0%
选择题
7
35.0%
解答题
1
5.0%
知识点统计
知识点
数量
占比
一元一次不等式组
2
10.0%
二元一次方程组单元测试
1
5.0%
数学竞赛
3
15.0%
相似单元测试
1
5.0%
圆单元测试
3
15.0%
二次函数单元测试
2
10.0%
二次根式单元测试
1
5.0%
实数单元测试
1
5.0%
一元二次方程单元测试
2
10.0%
平面四边形单元测试
1
5.0%
点和圆、直线和圆的位置关系
1
5.0%
多边形及其内角相和
1
5.0%
消元 解二元一次方程组
1
5.0%
版权提示
该作品由: 用户开绍清分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。