在实数 , 0 ,
,
中,无理数是( )
A . B . 0 C .
D .
D
【分析】
根据无理数的定义,即可求解.
【详解】
解:在实数 , 0 ,
,
中,无理数是
,
故选 D .
【点睛】
本题主要考查无理数的定义,掌握 “ 无限不循环小数是无理数 ” ,是解题的关键.
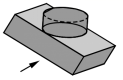
如图是由一个圆柱和一个长方体组成的几何体,则该几何体的俯视图是( )
A . 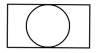 B .
B . ![]() C .
C . ![]() D .
D . ![]()
A
【分析】
根据从上边看得到的图形是俯视图,可得答案.
【详解】
解:俯视图是矩形中间有一个圆,圆与两个长相切,
故选: A .
【点睛】
此题主要考查了简单几何体的三视图,画简单组合体的三视图要通过仔细观察和想象.
若等式 + ( ) =
成立,则括号中填写单项式可以是( )
A . B .
C .
D .
C
【分析】
根据同底数幂的乘法法则以及合并同类项法则,即可求解.
【详解】
解: ∵ -
=
-
=
,
∴ 等式 + (
) =
成立,
故选 C .
【点睛】
本题主要考查整式的加减运算,掌握同底数幂的乘法法则以及合并同类项法则,是解题的关键.
阅读下列材料,其 ① ~ ④ 步中数学依据错误的是( )
| 如图:已知直线 证明: ①∵ ∴ ② 又 ∵ ③∴ ∴ ④∴ |
A . ① B . ② C . ③ D . ④
C
【分析】
根据垂直的定义和平行线的性质进行判断即可
【详解】
解:证明: ①∵ (已知)
∴ (垂直的定义)
② 又 ∵ (已知)
③∴ (两直线平行,同位角相等)
∴ (等量代换)
④∴ (垂直的定义).所以错在 ③
故选: C
【点睛】
本题考查了垂直的定义和平行线的性质,熟练掌握平行线的性质是解题的关键.
若点 关干
轴的对称点在第四象限,则
的取值范围在数轴上表示为( )
A . 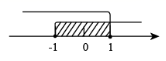 B .
B . 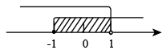
C . 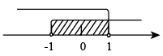 D .
D . ![]()
C
【分析】
先根据题意求出点 关于
轴的对称点
坐标,根据点
在第四象限列方程组,求解即可 .
【详解】
∵
∴ 点 关于
轴的对称点
坐标为
∵ 在第四象限
∴
解得:
故选: C
【点睛】
本题考查点关于坐标轴对称点求法,以及根据象限点去判断参数的取值范围,能根据题意找见相关的关系是解题关键.
本卷还有19题,登录并加入会员即可免费使用哦~

该作品由: 用户刘逢雪分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益,请联系 可圈可点 ,我们核实后将及时进行处理。