初中数学七年级上2020-2021学年度——第一章有理数综合复习题含详解
初中
整体难度：中等
2021-03-26
题号
一
二
三
四
五
评分
一、选择题 (共44题)
添加该题型下试题
1.
国务院总理李克强在 2020 年 5 月 22 日政府报告中说，去年我国农村贫困人口城少 11090000 ，脱贫攻坚取得决定性成就，数据 11090000 用科学记数法表示为（ ）
A ． B ．
C ．
D ．
难度：
知识点：有理数的乘除法
使用次数：208
【答案】
C
【分析】
科学记数法的表示形式为 a ×10 n 的形式，其中 1≤| a | ＜ 10 ， n 为整数．确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位， n 的绝对值与小数点移动的位数相同．当原数绝对值＞ 10 时， n 是正数；当原数的绝对值＜ 1 时， n 是负数．
【详解】
解： 11090000=1.109×10 7 ，
故选： C ．
【点睛】
此题考查科学记数法的表示方法．科学记数法的表示形式为 a ×10 n 的形式，其中 1≤| a | ＜ 10 ， n 为整数，表示时关键要正确确定 a 的值以及 n 的值．
2.
计算 的结果是（ ）
A ． 2 B ． 32 C ． D ．
难度：
知识点：有理数的乘除法
使用次数：264
【答案】
B
【分析】
将除法转化为乘法，再计算．
【详解】
解：
=
=32 ，
故选 B ．
【点睛】
本题考查了有理数的除法运算，解题的关键是掌握运算法则．
3.
－ 3 的相反数是（ ）
A ． B ． 3 C ．－ 3 D ．
难度：
知识点：有理数
使用次数：122
【答案】
B
【分析】
依据相反数的定义求解即可．
【详解】
解： 的相反数是 3 ，
故选： B ．
【点睛】
本题主要考查的是相反数的定义，掌握相反数的定义是解题的关键．
4.
为解决村庄灌溉问题，政府投资由水库向 ，
，
，
，
这五个村庄铺设管道，现已知这五个村庄与水库以及村与村之间的距离（单位：
）如图所示，则把水库的水输送到这五个村庄铺设管道的总长度最短应是（ ）
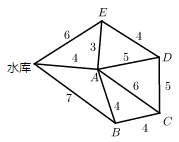
A ． B ．
C ．
D ．
难度：
知识点：有理数
使用次数：137
【答案】
A
【分析】
尽量选择数据较小的路线，到达 5 个村庄即可．
【详解】
解：如图，要使水管最短，一定要挑选最短的路程，
最短总长度应该是：
水库到 A ，再从 A 到 E 、 B ，同时从 B 到 C ，从 E 到 D ，
总长度为： 4+3+4+4+4=19km ，
故选 A ．
【点睛】
本题考查了最短路径问题，找到最短路线是解决本题的关键．
5.
据统计，绍兴市去年接待旅游人数约为 89000000 人，用科学记数法表示 89000000 为（ ）
A ． B ．
C ．
D ．
难度：
知识点：有理数的乘除法
使用次数：204
【答案】
C
【分析】
科学记数法的表示形式为 a ×10 n 的形式，其中 1≤| a | ＜ 10 ， n 为整数．确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位， n 的绝对值与小数点移动的位数相同．
【详解】
解： 89000000 这个数据用科学记数法表示为 8.9×10 7 ．
故选： C ．
【点睛】
此题考查科学记数法的表示方法．科学记数法的表示形式为 a ×10 n 的形式，其中 1≤| a | ＜ 10 ， n 为整数，表示时关键要正确确定 a 的值以及 n 的值．
本卷还有95题，登录并加入会员即可免费使用哦～
立即下载
全选试题
编辑试卷
收藏试卷
试题总数：
100
总体难度：
中等
难度统计
难度系数
数量
占比
基础
34
34.0%
容易
42
42.0%
中等
14
14.00%
很难
10
10.0%
题型统计
大题类型
数量
占比
选择题
44
44.0%
填空题
34
34.0%
解答题
22
22.0%
知识点统计
知识点
数量
占比
有理数的乘除法
41
41.0%
有理数
42
42.0%
正数和负数
4
4.0%
有理数的乘方
5
5.0%
有理数的加减法
8
8.0%
版权提示
该作品由: 用户区夜分享上传
可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系 可圈可点 ，我们核实后将及时进行处理。