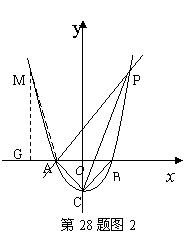
如图11所示，已知抛物线
与
轴交于A、B两点，与
轴交于点C．
（1）求A、B、C三点的坐标．
（2）过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．
（3）在轴上方的抛物线上是否存在一点M，过M作MG
轴
于点G，使以A、M、G三点为顶点的三角形与
PCA相似．
若存在，请求出M点的坐标；否则，请说明理由．
答案
解：（1）令
，得
解得
令
，得
∴ A
B
C
・・・・ （2分）
（2）∵OA=OB=OC=
∴
BAC=ACO=BCO=
∵AP∥CB， ∴PAB=
过点P作PE轴于E，则APE为等腰直角三角形
令OE=
，则PE=
∴P
∵点P在抛物线上 ∴
解得
，
（不合题意，舍去）
∴PE=
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ 4分）
∴四边形ACBP的面积
=
AB•OC+AB•PE
=
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ 6分）
(3)． 假设存在
∵PAB=BAC = ∴PAAC
∵MG轴于点G， ∴MGA=PAC =
在Rt△AOC中，OA=OC= ∴AC=
在Rt△PAE中，AE=PE= ∴AP= 
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ 7分）
设M点的横坐标为
，则M 
①点M在轴左侧时，则
() 当AMG 
PCA时，有
=
∵AG=
，MG=
即
解得
（舍去） 
（舍去）
() 当MAG PCA时有
=
即 
解得：
（舍去） 
∴M
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ （10分）
② 点M在轴右侧时，则
() 当AMG PCA时有=
∵AG=
，MG=
∴ 
解得（舍去） 
∴M
() 当MAGPCA时有=
即 
解得：（舍去） 
∴M
∴存在点M，使以A、M、G三点为顶点的三角形与PCA相似
M点的坐标为，， ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ （13分）
