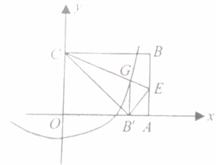
如图，在平面直角坐标系中，矩形OABC的顶点A（0，3），C（
，0）．将矩形OABC绕原点顺时针旋转90°，得到矩形
．设直线
与
轴交于点M、与
轴交于点N，抛物线
的图象经过点C、M、N．解答下列问题：
（1）分别求出直线和抛物线所表示的函数解析式；
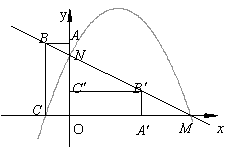
（2）将△MON沿直线MN翻折，点O落在点P处，请你判断点P是否在抛物线上，说明理由．
（3）将抛物线进行平移，使它经过点
，求此时抛物线的解析式．
 |
（1）由题意得，B（，3），
（3，1），∴直线的解析式为
；直线与轴的交点为M（5，0），与轴的交点N（0，
），设抛物线的解析式为
，∵抛物线过点N，∴
，∴
，∴抛物线的解析式为
=
；
（2）将△MON沿直线MN翻折，点O落在点P处，则P为（2，4），点P不在抛物线上；
（3）若抛物线上下平移经过点，此时解析式为
；当
时，
，∴
，
=
，若抛物线向左平移经过点，平移距离为
，此时解析式为
=
；若抛物线向右平移经过点，此时解析式为
。
（a，b，c是常数，a≠0），那么y叫做x 的二次函数。 （a≠0）中x、y是变量，a，b，c是常数，自变量x 的取值范围是全体实数，b和c可以是任意实数，a是不等于0的实数，因为a=0时，变为y=bx+c若b≠0,则y=bx+c是一次函数，若b=0，则y=c是一个常数函数。（a≠0）与一元二次方程（a≠0）有密切联系，如果将变量y换成一个常数，那么这个二次函数就是一个一元二次函数。（a，b，c是常数，a≠0），那么y叫做x 的二次函数。 
（a，b，c是常数，a≠0）； 
（a，h，k是常数，a≠0） 
与x轴有交点时，即对应二次好方程
有实根x1和x2存在时，根据二次三项式的分解因式
，二次函数
可转化为两根式
。如果没有交点，则不能这样表示。 （a，b，c是常数，a≠0）； （a，h，k是常数，a≠0） 与x轴有交点时，即对应二次好方程有实根x1和x2存在时，根据二次三项式的分解因式，二次函数可转化为两根式。如果没有交点，则不能这样表示。 （a≠0）的形式，那么这个函数就是二次函数，否则就不是。登录并加入会员可无限制查看知识点解析
x2+3共有的性质是( )