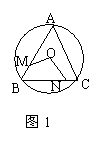在△ABC中,![]() BAC=90º,AB=AC=2
BAC=90º,AB=AC=2![]() ,圆A半径为1,如图所示。若点O在BC边上运动(与点B,C不重合),设BO=
,圆A半径为1,如图所示。若点O在BC边上运动(与点B,C不重合),设BO=![]() ,
,![]() AOC的面积为
AOC的面积为![]() 。
。
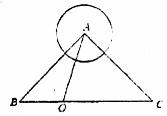
(1)求![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围。
的取值范围。
(2)以点O为圆心,BO长为半径作圆O,求当圆O与圆A相切时,![]() AOC的面积。
AOC的面积。
答案
解:(1) 过点A作AH![]() BC于H
BC于H
∵![]() BAC=90º,AB=AC=2
BAC=90º,AB=AC=2![]()
∴BC=4,AH=![]() BC=2
BC=2
∴S![]() ADC=
ADC=![]() AH
AH![]() CO=4
CO=4![]()
即![]() (0<
(0<![]() <4)
<4)
(2) 当点O与点H重合时,⊙O与⊙A相交,不合题意
当点O与点H不重合时,在Rt△AOH中
![]()
∵⊙A的半径为1,⊙O的半径为![]()
∴①当⊙A与外⊙O切时,AO=![]()
![]() 解得
解得![]()
此时![]() ADC的面积
ADC的面积![]()
②当⊙A与⊙O内切时,AO=![]()
∴![]() ,解得
,解得![]()
此时,![]() AOC的面积
AOC的面积![]()
∴当当⊙A与⊙O内切时,![]() AOC的面积为
AOC的面积为![]() 或
或![]()

 。
。