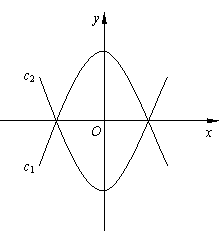
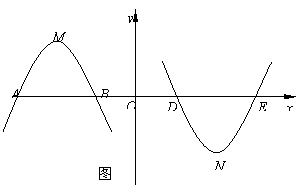
将抛物线c₁：y=沿x轴翻折，得抛物线c₂，如图所示.

（1）请直接写出抛物线c₂的表达式.

（2）现将抛物线c₁向左平移m个单位长度，平移后得到的新抛物线的顶点为M，与x轴的交点从左到右依次为A，B；将抛物线c₂向右也平移m个单位长度，平移后得到的新抛物线的顶点为N，与x轴交点从左到右依次为D，E.

①当B，D是线段AE的三等分点时，求m的值；

②在平移过程中，是否存在以点A，N，E，M为顶点的四边形是矩形的情形？若存在，请求出此时m的值；若不存在，请说明理由.

答案

解：（1）.     

（2）①令，得：，

               则抛物线c₁与轴的两个交点坐标为（-1,0），（1,0）.

∴A（-1-m，0），B（1-m，0）.

同理可得：D（-1+m，0），E（1+m，0）.

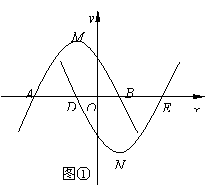
当时，如图①，

，∴.                    

当时，如图②，，

 ∴.                 ∴当或2时，B，D是线段AE的三等分点. 

②存在.                                     

方法一

理由：连接AN、NE、EM、MA.依题意可得：.

即M，N关于原点O对称，  ∴.

∵， ∴A，E关于原点O对称，   ∴，

∴四边形ANEM为平行四边形.                 

要使平行四边形ANEM为矩形，必需满足,

即，       ∴.

∴当时，以点A，N，E，M为顶点的四边形是矩形.

方法二

理由：连接AN、NE、EM、MA. 依题意可得：.

即M，N关于原点O对称，  ∴.

∵， ∴A，E关于原点O对称，   ∴，

∴四边形ANEM为平行四边形.   

∵，

，

，

若，则，∴.

此时△AME是直角三角形，且∠AME=90°.

∴当时，以点A，N，E，M为顶点的四边形是矩形.