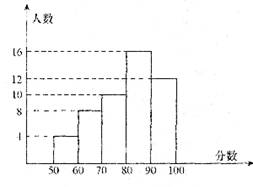
为了让广大青少年学生走向操场、走进自然、走到阳光下，积极参加体育锻炼，我国启动了“全国亿万学生阳光体育运动”．短跑运动，可以锻炼人的灵活性，增强人的爆发力，因此小明和小亮在课外活动中，报名参加了短跑训练小组．在近五次百米训练中，所测成绩如图所示，请根据图中所示解答以下问题．
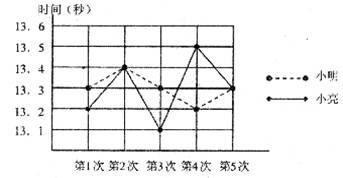
(1)请根据图中信息，补齐下面的表格；
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 小明 | 13.3 | 13.4 | 13.3 | 13.3 | |
| 小亮 | 13.2 | 13.1 | 13.5 | 13.3 |
(2)从图中看, 小明与小亮哪次的成绩最好?
(3)分别计算他们的平均数、极差和方差；若你是他们的教练，将小明与小亮的成绩比较后，你将分别给予他们怎样的建议?
答案
解：（1）小明l3．2；小亮13． 4．
(2)小亮第4次成绩最好，小明第2次成绩最好。
(3)
小明==I(13．3+13．4+13．3+13．2+13．3)=13．3；
小亮==1(13．2+13．4+13．1+13．5+13．3)=13．3．
小明的数据极差：l3．4―13．2＝0．2；
小亮的数据极差：l3．5―13．1=0．4：
S2 小明=
S2小亮=0．02
