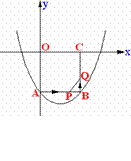
如图所示，在平面直角坐标系xOy中，正方形OABC的边长为2cm，点A、C分别在y轴的负半轴和x轴的正半轴上，抛物线y=ax²+bx+c经过点A、B和D.

（1）求抛物线的解析式.  

（2）如果点P由点A出发沿AB边以2cm/s的速度向点B运动，同

时点Q由点B出发沿BC边以1cm/s的速度向点C运动，当其中一点到达终点时，另一点也随之停止运动. 设S=PQ²(cm²)

①试求出S与运动时间t之间的函数关系式，并写出t的取值范围；

②当S取时，在抛物线上是否存在点R，使得以P、B、Q、R为顶点的四边形是平行四边形?  如果存在，求出R点的坐标；如果不存在，请说明理由. 

（3）在抛物线的对称轴上求点M，使得M到D、A的距离之差最大，求出点M的坐标. 中

答案

解: (1)据题意知: A(0, －2), B(2, －2) ，D（4，—）, 

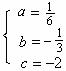
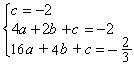
则                                  解得                    

     ∴抛物线的解析式为:  …… 3分（三个系数中，每对1个得1分）

  (2) ①由图象知: PB=2－2t, BQ= t, ∴S=PQ²=PB²+BQ²=(2－2t)² + t² ,

即 S=5t²－8t+4 (0≤t≤1)   …… 2分（解析式和t取值范围各1分）

②假设存在点R, 可构成以P、B、R、Q为顶点的平行四边形.

∵S=5t²－8t+4 (0≤t≤1),  ∴当S=时,  5t²－8t+4=,得 20t²－32t+11=0,

解得 t = ，t = （不合题意，舍去） …… 2分

此时点 P的坐标为（1，-2），Q点的坐标为（2，—）

若R点存在，分情况讨论:

【A】假设R在BQ的右边, 这时QRPB, 则，R的横坐标为3, R的纵坐标为—

 即R (3, －)，代入, 左右两边相等，

∴这时存在R(3, －)满足题意. …… 1分

【B】假设R在BQ的左边, 这时PRQB, 则：R的横坐标为1, 纵坐标为－即(1, －)  代入, 左右两边不相等, R不在抛物线上. …… 1分

【C】假设R在PB的下方, 这时PRQB, 则：R(1，—)代入,

 左右不相等, ∴R不在抛物线上. …… 1分

    综上所述, 存点一点R(3, －)满足题意.

（3）∵A关于抛物线的对称轴的对称点为B,过B、D的直线与抛物线的对称轴的交点为所求M，M的坐标为（1，—）…… 2分