和
都是等边三角形.
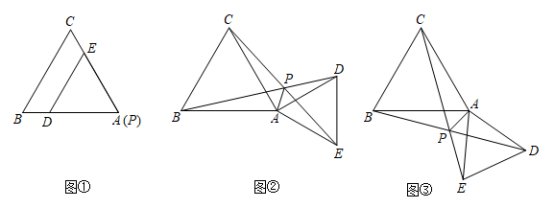
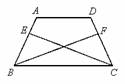
(1) 将 绕点 A 旋转到图 ① 的位置时,连接 BD , CE 并延长相交于点 P (点 P 与点 A 重合),有
(或
)成立;请证明.
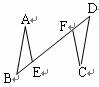
(2) 将 绕点 A 旋转到图 ② 的位置时,连接 BD , CE 相交于点 P ,连接 PA ,猜想线段 PA 、 PB 、 PC 之间有怎样的数量关系?并加以证明;
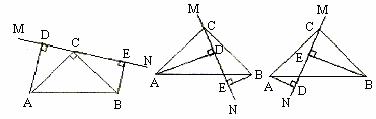
(3) 将 绕点 A 旋转到图 ③ 的位置时,连接 BD , CE 相交于点 P ,连接 PA ,猜想线段 PA 、 PB 、 PC 之间有怎样的数量关系?直接写出结论,不需要证明.
答案
(1) 证明见解析
(2) 图 ② 结论: ,证明见解析
(3) 图 ③ 结论:
【分析】( 1 )由 △ ABC 是等边三角形,得 AB = AC ,再因为点 P 与点 A 重合,所以 PB = AB , PC = AC , PA =0 ,即可得出结论;
( 2 )在 BP 上截取 ,连接 AF ,证明
( SAS ),得
,再证明
( SAS ),得
,
,然后证明
是等边三角形,得
,即可得出结论;
( 3 )在 CP 上截取 ,连接 AF ,证明
( SAS ),得
,再证明
( SAS ),得出
,
,然后证明
是等边三角形,得
,即可得出结论:
.
【详解】( 1 )证明: ∵△ ABC 是等边三角形,
∴ AB = AC ,
∵ 点 P 与点 A 重合,
∴ PB = AB , PC = AC , PA =0 ,
∴ 或
;
( 2 )解:图 ② 结论:
证明:在 BP 上截取 ,连接 AF ,
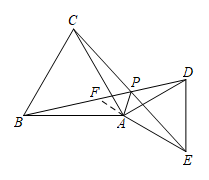
∵ 和
都是等边三角形,
∴ ,
,
∴ ,
∴ ,
∴ ( SAS ),
∴ ,
∵ AC = AB , CP = BF ,
∴ ( SAS ),
∴ ,
,
∴ ,
∴ ,
∴ 是等边三角形,
∴ ,
∴ ;
( 3 )解:图 ③ 结论: ,
理由:在 CP 上截取 ,连接 AF ,
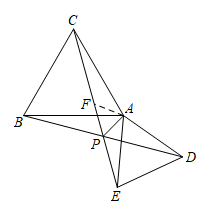
∵ 和
都是等边三角形,
∴ ,
,
∴ ,
∴ ,
∴ ( SAS ),
∴ ,
∵ AB = AC , BP = CF ,
∴ ( SAS ),
∴ ,
,
∴ ,
∴ ,
∴ 是等边三角形,
∴ ,
∴ ,
即 .
【点睛】本题考查等边三角形的判定与性质,全等三角形的判定与性质,熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键.