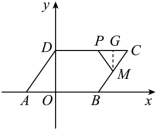
如图，在平面直角坐标系中，平行四边形 ABCD 的边 AB 在 x 轴上，顶点 D 在 y 轴的正半轴上， M 为 BC 的中点， OA 、 OB 的长分别是一元二次方程 的两个根 ， ，动点 P 从点 D 出发以每秒 1 个单位长度的速度沿折线 向点 B 运动，到达 B 点停止．设运动时间为 t 秒， 的面积为 S ．

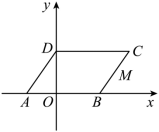
(1) 求点 C 的坐标；

(2) 求 S 关于 t 的函数关系式，并写出自变量 t 的取值范围；

(3) 在点 P 的运动过程中，是否存在点 P ，使 是等腰三角形？若存在，请直接写出点 P 的坐标；若不存在，请说明理由．

答案

(1) 点 C 坐标为

(2)

(3) 存在点 P 或 或 ，使 是等腰三角形

【分析】（ 1 ）先求出方程的解，可得 ， ，再由 ，可得 ，然后根据四边形 ABCD 是平行四边形，可得 CD =7 ， ，即可求解；

（ 2 ）分两种情况讨论：当 时，当 时，过点 A 作 交 CB 的延长线于点 F ，即可求解；

（ 3 ）分三种情况讨论：当 CP = PM 时，过点 M 作 MF ⊥ PC 于点 F ；当 时；当 PM = CM 时，过点 M 作 MG ⊥ PC 于点 G ，即可求解．

【详解】（ 1 ）解： ，解得 ， ，

∵ ，

∴ ， ，

∵ ，

∴ ，

∴ ，

∵ 四边形 ABCD 是平行四边形，

∴ ， ，

∴ 点 C 坐标为 ；

（ 2 ）解：当 时， ，

当 时，过点 A 作 交 CB 的延长线于点 F ，如图，

，

∵ 四边形 ABCD 是平行四边形，

∴ ，

∵ ，

∴ ，

∴ ，

∴ ，

∴ ；

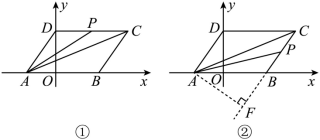
（ 3 ）解：存在点 P ，使 是等腰三角形，理由如下：

根据题意得：当点 P 在 CD 上运动时， 可能是等腰三角形，

∵ 四边形 ABCD 是平行四边形，

∴∠ C =∠ BAD ， BC = AD =5 ，

∴ ，

∵ 点 M 为 BC 的中点，

∴ ，

当 CP = PM 时，过点 M 作 MF ⊥ PC 于点 F ，

∴ ，

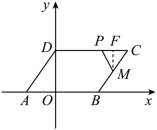
设 PC = PM = a ，则 PD =7- a ， ，

∵ PF ² + FM ² = PM ² ，

∴ ，解得： ，

∴ ，

∴ 此时点 P ；

当 时，

∴ ，

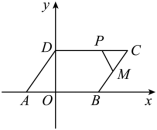
∴ 此时点 P ；

当 PM = CM 时，过点 M 作 MG ⊥ PC 于点 G ，则 ，

∴ ，

∴ PD =7- PC =4 ，

∴ 此时点 P ；

综上所述，存在点 P 或 或 ，使 是等腰三角形

【点睛】本题主要考查了平行四边形的性质，坐标与图形，等腰三角形的性质，解直角三角形，熟练掌握相关知识点，并利用数形结合思想解答是解题的关键．