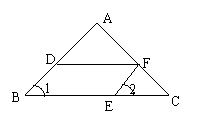
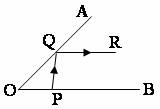
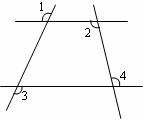
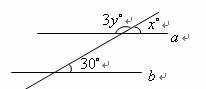
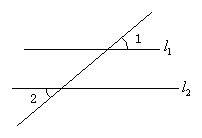
如图，如果，那么，其

当前位置：

学科首页

七下第五章相交线与平行线

平行线及其判定

试题详情

难度：

使用次数：168

更新时间：2023-05-19

纠错

如图，如果，那么，其依据可以简单说成（）

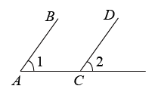
A ．两直线平行，内错角相等 B ．内错角相等，两直线平行

C ．两直线平行，同位角相等 D ．同位角相等，两直线平行

查看答案

题型：选择题

知识点：平行线及其判定

下载试题

复制试题

【答案】

【分析】根据 “ 同位角相等，两直线平行 ” 即可得．

【详解】解：因为与是一对相等的同位角，得出结论是，

所以其依据可以简单说成同位角相等，两直线平行，

故选： D ．

【点睛】本题考查了平行线的判定，熟练掌握平行线的判定方法是解题关键．

考点梳理:

根据可圈可点权威老师分析，试题“ ”主要考查你对平行线的判定等考点的理解。关于这些考点的“资料梳理”如下：

◎ 平行线的判定的定义

平行线的概念：
在同一个平面内，不相交的两条直线叫做平行线。平行用符号“∥，如“AB∥CD”，读作“AB平行于CD”。
注意：
①平行线是无限延伸的，无论怎样延伸也不相交。
②当遇到线段、射线平行时，指的是线段、射线所在的直线平行。

◎ 平行线的判定的知识扩展

1、平行线的概念：在同一个平面内，不相交的两条直线叫做平行线。平行用符号“∥，如“AB∥CD”，读作“AB平行于CD”。
注意：（1）平行线是无限延伸的，无论怎样延伸也不相交。
（2）当遇到线段、射线平行时，指的是线段、射线所在的直线平行。
2、平行线的判定平行线的判定公理：
（1）两条直线被第三条直线所截，如果同位角相等，那么两直线平行。简称：同位角相等，两直线平行。
（2）两条直线被第三条直线所截，如果内错角相等，那么两直线平行。简称：内错角相等，两直线平行。
（3）两条直线被第三条直线所截，如果同旁内角互补，那么两直线平行。简称：同旁内角互补，两直线平行。
还有下面的判定方法：
（1）平行于同一条直线的两直线平行。
（2）垂直于同一条直线的两直线平行。
（3）平行线的定义。

◎ 平行线的判定的知识点拨

平行线的判定平行线的判定公理：
（1）两条直线被第三条直线所截，如果同位角相等，那么两直线平行。简称：同位角相等，两直线平行。
（2）两条直线被第三条直线所截，如果内错角相等，那么两直线平行。简称：内错角相等，两直线平行。
（3）两条直线被第三条直线所截，如果同旁内角互补，那么两直线平行。简称：同旁内角互补，两直线平行。
还有下面的判定方法：
（1）平行于同一条直线的两直线平行。
（2）垂直于同一条直线的两直线平行。
（3）平行线的定义。

判定方法的逆应用：
在同一平面内，两直线不相交，即平行。
两条直线平行于一条直线，则三条不重合的直线互相平行。
两直线平行，同位角相等。
两直线平行，内错角相等。
两直线平行，同旁内角互补。
6a⊥c，b⊥c则a∥b。

◎ 平行线的判定的教学目标

1、熟练掌握平行线的三个判定方法，并会运用。
2、遇到一个新问题时，能把它转化为已知的（或已解决的）问题。
3、感受数学来源于生活，激发学学习数学的兴趣，培养逻辑思维。

◎ 平行线的判定的考试要求

能力要求：掌握
课时要求：60
考试频率：必考
分值比重：3

开通会员

登录并加入会员可无限制查看知识点解析

类题推荐：

平行线及其判定

难度：

使用次数：87

更新时间：2021-07-15