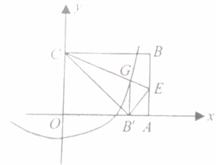
在平面直角坐标系中，抛物线 （ b 是常数）经过点 ．点 A 在抛物线上，且点 A 的横坐标为 m （ ）．以点 A 为中心，构造正方形 ， ，且 轴．

(1) 求该抛物线对应的函数表达式：

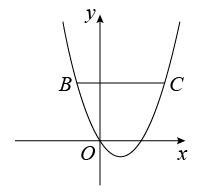
(2) 若点 B 是抛物线上一点，且在抛物线对称轴左侧．过点 B 作 x 轴的平行线交抛物线于另一点 C ，连接 ．当 时，求点 B 的坐标；

(3) 若 ，当抛物线在正方形内部的点的纵坐标 y 随 x 的增大而增大时，或者 y 随 x 的增大而减小时，求 m 的取值范围；

(4) 当抛物线与正方形 的边只有 2 个交点，且 交点 的纵坐标之差为 时，直接写出 m 的值．

答案

(1)

(2)

(3) 或

(4) 或 或 ．

【分析】（ 1 ）将点 代入 ，待定系数法求解析式即可求解；

（ 2 ）设 ，根据对称性可得 ，根据 ，即可求解；

（ 3 ）根据题意分两种情况讨论，分别求得当正方形 点 在 轴上时，此时 与 点重合，当 经过抛物线的对称轴 时，进而观察图像即可求解；

（ 4 ）根据题意分三种情况讨论，根据正方形的性质以及点的坐标位置，即可求解．

（ 1 ）

解： ∵ 抛物线 （ b 是常数）经过点

∴

解得

（ 2 ）

如图，

由

则对称轴为直线 ，

设 ，则

解得

（ 3 ）

点 A 在抛物线上，且点 A 的横坐标为 m （ ）．以点 A 为中心，构造正方形 ， ，且 轴

，且 在 轴上，如图，

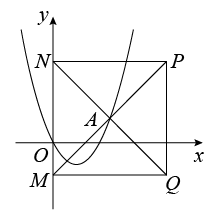
① 当抛物线在正方形内部的点的纵坐标 y 随 x 的增大而增大时，如图，当正方形 点 在 轴上时，此时 与 点重合，

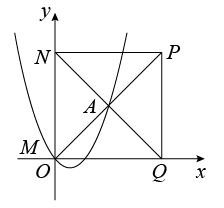
的解析式为

，将 代入

即

解得

观察图形可知，当 时，抛物线在正方形内部的点的纵坐标 y 随 x 的增大而增大；

② 当抛物线在正方形内部的点的纵坐标 y 随 x 的增大而减小时，当 经过抛物线的对称轴 时，

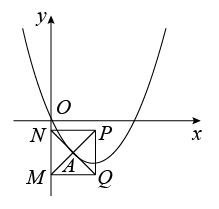
解得 ，

观察图形可知，当 时，抛物线在正方形内部的点的纵坐标 y 随 x 的增大而增大；

综上所述， m 的取值范围为 或

（ 4 ）

① 如图，设正方形与抛物线的交点分别为 ，当 时，则

是正方形 的中心，

即

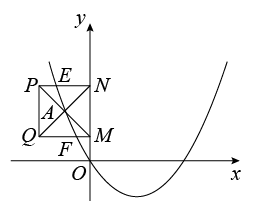
② 如图，当 点在抛物线对称轴左侧， 轴右侧时，

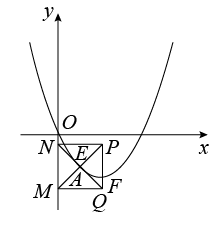
交点的纵坐标之差为 ，

的纵坐标为

的横坐标为

在抛物线 上，

解得

③ 当 在抛物线对称轴的右侧时，正方形与抛物线的交点分别为 ， ，设直线 交 轴于点 ，如图，

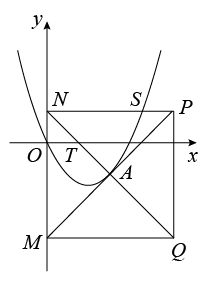
则

即

设直线 解析式为

则

解得

直线 解析式为

联立

解得 （舍去）

即 的横坐标为 ，即 ，

综上所述， 或 或 ．

【点睛】本题考查了二次函数的综合问题，二次函数的对称性，正方形的性质，掌握二次函数图像的性质是解题的关键．