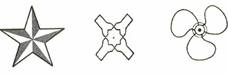
下列图形是中心对称图形的是（）

当前位置：

学科首页

九上第二十三章旋转

中心对称

试题详情

难度：

使用次数：296

更新时间：2023-05-18

纠错

下列图形是中心对称图形的是（）

A ． B ． C ． D ．

查看答案

题型：选择题

知识点：中心对称

下载试题

复制试题

【答案】

【分析】根据中心对称图形的定义（在平面内，把一个图形绕某点旋转，如果旋转后的图形与另一个图形重合，那么这两个图形互为中心对称图形）逐项判断即可得．

【详解】解： A 、不是中心对称图形，此项不符合题意；

B 、是中心对称图形，此项符合题意；

C 、不是中心对称图形，此项不符合题意；

D 、不是中心对称图形，此项不符合题意；

故选： B ．

【点睛】本题考查了中心对称图形，熟记中心对称图形的定义是解题关键．

考点梳理:

根据可圈可点权威老师分析，试题“ ”主要考查你对中心对称等考点的理解。关于这些考点的“资料梳理”如下：

◎ 中心对称的定义

中心对称的定义：
把一个图形绕着某一个点旋转180°，如果它能够与另一个图形重合，那么说这两个图形关于这个点中心对称，这个点叫做对称中心。
中心对称图形的定义：
在平面内，一个图形绕着某一个点旋转180°，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心。

◎ 中心对称的知识扩展

1、定义：把一个图形绕着某一个点旋转180°，如果它能够与另一个图形重合，那么说这两个图形关于这个点中心对称，这个点叫做对称中心。
2、中心对称的性质：
（1）关于中心对称的两个图形是全等形。
（2）关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。
（3）关于中心对称的两个图形，对应线段平行（或在同一直线上）且相等。
3、中心对称的判定：如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称。
4、中心对称图形的定义：在平面内，一个图形绕着某一个点旋转180°，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心。

◎ 中心对称的特性

中心对称的性质：
①关于中心对称的两个图形是全等形。
②关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。
③关于中心对称的两个图形，对应线段平行（或在同一直线上）且相等。

中心对称的判定：
如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称。

◎ 中心对称的知识对比

中心对称与中心对称图形的联系:
中心对称和中心对称图形是两个不同而又紧密联系的概念。
区别是：
中心对称是指两个全等图形之间的相互位置关系，这两个图形关于一点对称，这个点是对称中心，两个图形关于点的对称也叫做中心对称。成中心对称的两个图形中，其中一个图形上所有点关于对称中心的对称点都在另一个图形上，反之，另一个图形上所有点的对称点，又都在这个图形上；
而中心对称图形是指一个图形本身成中心对称。中心对称图形上所有点关于对称中心的对称点都在这个图形本身上。如果将中心对称的两个图形看成一个整体（一个图形），那么这个图形就是中心对称图形；一个中心对称图形，如果把对称的部分看成是两个图形，那么它们又是关于中心对称。
也就是说：
① 中心对称图形：如果把一个图形绕某一点旋转180度后能与自身重合，这个图形是中心对称图形。
②中心对称：如果把一个图形绕某一点旋转180度后能与另一个图形重合，这两个图形成中心对称。

◎ 中心对称的教学目标

1、理解中心对称，对称中心，对称点等概念；
2、掌握中心对称的性质；
3、应用中心对称的概念及性质，解决实际问题；
4、经历探究发现中心对称性质的过程，提高观察、分析、抽象、概括等能力；体验猜想、类比等数学思想。

◎ 中心对称的考试要求

能力要求：理解
课时要求：60
考试频率：选考
分值比重：3

开通会员

登录并加入会员可无限制查看知识点解析

类题推荐：

中心对称

难度：

使用次数：118

更新时间：2009-02-19

加入组卷

下面的图形中，是中心对称图形的是（　　）

A． B． C． D．

查看答案

题型：选择题

知识点：中心对称

复制

试题详情

纠错

难度：

使用次数：166

更新时间：2009-03-15

加入组卷

下列图形中，不是中心对称图形的是（）

A. 圆 B. 菱形 C. 矩形 D. 等边三角形

查看答案

题型：选择题

知识点：中心对称

复制

试题详情

纠错

难度：

使用次数：180

更新时间：2021-07-16

加入组卷

下面的扑克牌中，牌面是中心对称图形的是____________。（填序号）

查看答案

题型：填空题

知识点：中心对称

复制

试题详情

纠错

难度：

使用次数：152

更新时间：2009-03-15

加入组卷

下列各图中，是中心对称图形的是（　　）

A B C D

查看答案

题型：选择题

知识点：中心对称

复制

试题详情

纠错

难度：

使用次数：114

更新时间：2009-03-15

加入组卷

如图，在方格纸（每个小方格都是边长为1个单位长度的正方形）中，我们称每个小正方形的顶点为格点，以格点为顶点的图形称为格点图形．如图中的称为格点．

（1）如果两点的坐标分别是和，请你在方格纸中建立平面直角坐标系，并直接写出点，点的坐标；

（2）请根据你所学过的平移、旋转或轴对称等知识，说明图中“格点四边形图案”是如何通过“格点图案”变换得到的．

查看答案

题型：解答题

知识点：中心对称

复制

试题详情

纠错

加入组卷

进入组卷

下载知识点

使用过本题的试卷：

2022年浙江省衢州市中考数学真题1

知识点：

中心对称

版权提示

该作品由: 用户袁璞分享上传

可圈可点是一个信息分享及获取的平台。不确保部分用户上传资料的来源及知识产权归属。如您发现相关资料侵犯您的合法权益，请联系可圈可点，我们核实后将及时进行处理。