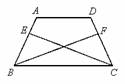
【思维探究】如图 1 ,在四边形 ABCD 中, ∠ BAD = 60° , ∠ BCD = 120° , AB = AD ,连接 AC .求证: BC + CD = AC .

(1) 小明的思路是:延长 CD 到点 E ,使 DE = BC ,连接 AE .根据 ∠ BAD +∠ BCD = 180° ,推得 ∠ B +∠ ADC = 180° ,从而得到 ∠ B = ∠ ADE ,然后证明 ADE ≌
ABC ,从而可证 BC + CD = AC ,请你帮助小明写出完整的证明过程.
(2) 【思维延伸】如图 2 ,四边形 ABCD 中, ∠ BAD = ∠ BCD = 90° , AB = AD ,连接 AC ,猜想 BC , CD , AC 之间的数量关系,并说明理由.
(3) 【思维拓展】在四边形 ABCD 中, ∠ BAD = ∠ BCD = 90° , AB = AD = , AC 与 BD 相交于点 O .若四边形 ABCD 中有一个内角是 75° ,请直接写出线段 OD 的长.
答案
(1) AC = BC + CD ;理由见详解;
(2) CB + CD = AC ;理由见详解;
(3) 或
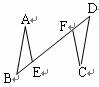
【分析】( 1 )如图 1 中,延长 CD 到点 E ,使 DE = BC ,连接 AE .证明 △ ADE ≌△ ABC ( SAS ),推出 ∠ DAE =∠ BAC , AE = AC ,推出 △ ACE 的等边三角形,可得结论;
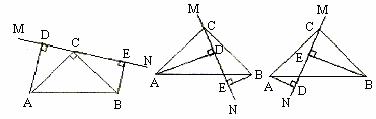
( 2 )结论: CB + CD = AC .如图 2 中,过点 A 作 AM ⊥ CD 于点 M , AN ⊥ CB 交 CB 的延长线于点 N .证明 △ AMD ≌△ ANB ( AAS ),推出 DM = BN , AM = AN ,证明 Rt △ ACM ≌ Rt △ ACN ( HL ),推出 CM = CN ,可得结论;
( 3 )分两种情形:如图 3-1 中,当 ∠ CDA =75° 时,过点 O 作 OP ⊥ CB 于点 P , CQ ⊥ CD 于点 Q .如图 3-2 中,当 ∠ CBD =75° 时,分别求解即可.
【详解】( 1 )证明:如图 1 中,延长 CD 到点 E ,使 DE = BC ,连接 AE .

∵∠ BAD +∠ BCD =180° ,
∴∠ B +∠ ADC =180° ,
∵∠ ADE +∠ ADC =180°
∴∠ B =∠ ADE ,
在 △ ADE 和 △ ABC 中,
,
∴△ ADE ≌△ ABC ( SAS ),
∴∠ DAE =∠ BAC , AE = AC ,
∴∠ CAE =∠ BAD =60° ,
∴△ ACE 的等边三角形,
∴ CE = AC ,
∵ CE = DE + CD ,
∴ AC = BC + CD ;
( 2 )解:结论: CB + CD = AC .
理由:如图 2 中,过点 A 作 AM ⊥ CD 于点 M , AN ⊥ CB 交 CB 的延长线于点 N .

∵∠ DAB =∠ DCB =90° ,
∴∠ CDA +∠ CBA =180° ,
∵∠ ABN +∠ ABC =180° ,
∴∠ D =∠ ABN ,
∵∠ AMD =∠ N =90° , AD = AB ,
∴△ AMD ≌△ ANB ( AAS ),
∴ DM = BN , AM = AN ,
∵ AM ⊥ CD , AN ⊥ CN ,
∴∠ ACD =∠ ACB =45° ,
∴ AC = CM ,
∵ AC = AC . AM = AN ,
∴ Rt △ ACM ≌ Rt △ ACN ( HL ),
∴ CM = CN ,
∴ CB + CD = CN BN + CM + DM =2 CM =
AC ;
( 3 )解:如图 3-1 中,当 ∠ CDA =75° 时,过点 O 作 OP ⊥ CB 于点 P , CQ ⊥ CD 于点 Q .
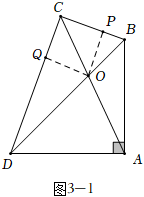
∵∠ CDA =75° , ∠ ADB =45° ,
∴∠ CDB =30° ,
∵∠ DCB =90° ,
∴ CD = CB ,
∵∠ DCO =∠ BCO =45° , OP ⊥ CB , OQ ⊥ CD ,
∴ OP = OQ ,
∴ ,
∴ ,
∵ AB = AD = , ∠ DAB =90° ,
∴ BD = AD =2
,
∴ OD = .
如图 3-2 中,当 ∠ CBD =75° 时,

同法可证 ,
,
综上所述,满足条件的 OD 的长为 或
.
【点睛】本题属于四边形综合题,考查了全等三角形的判定和性质,解直角三角形,等边三角形的判定和性质,角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.