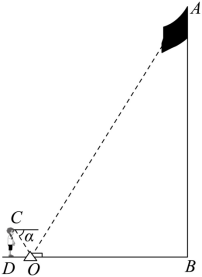
如图，为了测量校园内旗杆 AB 的高度，九年级数学应用实践小组，根据光的反射定律，利用镜子、皮尺和测角仪等工具，按以下方式进行测量：把镜子放在点 O 处，然后观测者沿着水平直线 BO 后退到点 D ，这时恰好能在镜子里看到旗杆顶点 A ，此时测得观测者观看镜子的俯角 α =60° ，观测者眼睛与地面距离 CD =1.7m ， BD =11m ，则旗杆 AB 的高度约为 _________m ．（结果取整数， ）

答案

17

【分析】如图容易知道 CD ⊥ BD ， AB ⊥ BD ，即 ∠ CDO =∠ ABO =90° ．由光的反射原理可知 ∠ COD =∠ AOB =60° ，这样可以得到 △ COD ∽△ AOB ，然后利用对应边成比例就可以求出 AB ．

【详解】解：由题意知 ∠ COD =∠ AOB =60° ， ∠ CDE =∠ ABE =90° ，

∵ CD =1.7 m ，

∴ OD = ≈1(m) ，

∴ OB =11-1=10(m) ，

∴△ COD ∽△ AOB ．

∴ ，即 ，

∴ AB =17(m) ，

答：旗杆 AB 的高度约为 17m ．

故答案为： 17 ．

【点睛】本题考查了解直角三角形的应用，相似三角形的应用，本题只要是把实际问题抽象到相似三角形中，利用相似三角形的性质就可以求出结果．