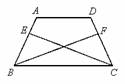
如图,在平行四边形 中,
是一条对角线,且
,
,
,
是
边上两点,点
在点
的右侧,
,连接
,
的延长线与
的延长线相交于点
.
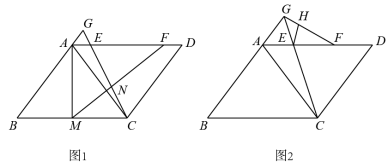
(1) 如图 1 , 是
边上一点,连接
,
,
与
相交于点
.
① 若 ,求
的长;
② 在满足 ① 的条件下,若 ,求证:
;
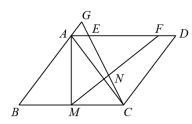
(2) 如图 2 ,连接 ,
是
上一点,连接
.若
,且
,求
的长.
答案
(1)① ; ② 证明见解析
(2)
【分析】( 1 ) ① 解:根据平行四边形 的性质可证
,得到
,再根据
,
,
,结合平行四边形的性质求出
的长,代入比例式即可求出
的长;
② 先根据 证明
可得
,再根据
,
求出
,进一步证明
,最后利用等腰三角形的三线合一可证明结论.
( 2 )如图,连接 ,先根据
证明
,再结合
,说明
,利用平行线分线段成比例定理可得
,接着证明
,可得到
,设
,则
,根据
构建方程求出
,最后利用
可得结论.
【详解】( 1 ) ① 解:如图,
∵ 四边形 是平行四边形,
,
,
∴ ,
,
,
,
∴ ,
,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ 的长为
.
② 证明: ∵ ,
∴ ,
∵ ,
在 和
中,
∴ ,
∴ ,
∵ ,
,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ .
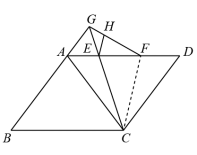
( 2 )如图,连接 ,
∵ ,
,
∴ ,
∴ ,
∵ ,
在 和
中,
∴ ,
∴ ,
∴
∵ ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
,
∴ ,
∴ ,
∴ ,
∴ ,
设 ,则
,
∵ ,
∴ ,
∴ ,
即 ,
∴ ,
∴ .
∴ 的长为
.
 【点睛】本题考查了平行四边形的性质,相似三角形的判定及性质,全等三角形的判定及性质,等腰三角形的三线合一,平行线的判定及性质,平行线分线段成比例定理等知识.灵活运用相似三角形和全等三角形的判定及性质是解答本题的关键.
【点睛】本题考查了平行四边形的性质,相似三角形的判定及性质,全等三角形的判定及性质,等腰三角形的三线合一,平行线的判定及性质,平行线分线段成比例定理等知识.灵活运用相似三角形和全等三角形的判定及性质是解答本题的关键.