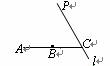
如图,在 △ ABC 中, ∠ ABC= 40° , ∠ ACB= 90° , AE 平分 ∠ BAC 交 BC 于点 E . P 是边 BC 上的动点(不与 B , C 重合),连结 AP ,将 △ APC 沿 AP 翻折得 △ APD ,连结 DC ,记 ∠ BCD=α .
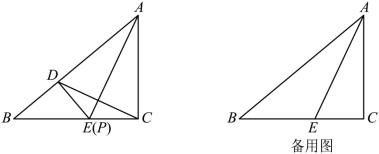
(1) 如图,当 P 与 E 重合时,求 α 的度数.
(2) 当 P 与 E 不重合时,记 ∠ BAD=β ,探究 α 与 β 的数量关系.
答案
(1)25°
(2)① 当点 P 在线段 BE 上时, 2 α - β = 50° ; ② 当点 P 在线段 CE 上时, 2 α + β = 50°
【分析】( 1 )由 ∠ B = 40° , ∠ ACB = 90° ,得 ∠ BAC = 50° ,根据 AE 平分 ∠ BAC , P 与 E 重合,可得 ∠ ACD ,从而 α = ∠ ACB −∠ ACD ;
( 2 )分两种情况: ① 当点 P 在线段 BE 上时,可得 ∠ ADC = ∠ ACD = 90°− α ,根据 ∠ ADC + ∠ BAD = ∠ B + ∠ BCD ,即可得 2 α − β = 50° ; ② 当点 P 在线段 CE 上时,延长 AD 交 BC 于点 F ,由 ∠ ADC = ∠ ACD = 90°− α , ∠ ADC = ∠ AFC + α = ∠ ABC + ∠ BAD + α 可得 90°− α = 40° + α + β ,即 2 α + β = 50° .
【详解】( 1 )解: ∵∠ B = 40° , ∠ ACB = 90° ,
∴∠ BAC = 50° ,
∵ P 与 E 重合, AE 平分 ∠ BAC ,
∴ D 在 AB 边上, AE ⊥ CD ,
∴∠ ACD = 65° ,
∴ α = ∠ ACB - ∠ ACD = 25° ;
( 2 ) ① 如图 1 ,当点 P 在线段 BE 上时,
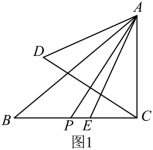
∵∠ ADC = ∠ ACD = 90° - α , ∠ ADC + ∠ BAD = ∠ B + ∠ BCD ,
∴90° - α + β = 40° + α ,
∴2 α - β = 50° ;
② 如图 2 ,当点 P 在线段 CE 上时,
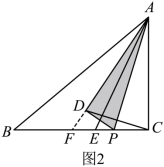
延长 AD 交 BC 于点 F ,
∵∠ ADC = ∠ ACD = 90° - α , ∠ ADC = ∠ AFC + α = ∠ ABC + ∠ BAD + α = 40° + α + β ,
∴90° - α = 40° + α + β ,
∴2 α + β = 50° .
【点睛】本题考查三角形综合应用,涉及轴对称变换,三角形外角等于不相邻的两个内角的和的应用,解题的关键是掌握轴对称的性质,能熟练运用三角形外角的性质.