如图,已知在 Rt △ ABC 中, , D 是 AB 边上一点,以 BD 为直径的半圆 O 与边 AC 相切,切点为 E ,过点 O 作
,垂足为 F .
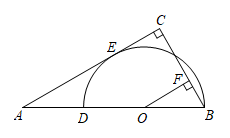
(1) 求证: ;
(2) 若 ,
,求 AD 的长.
答案
(1) 见解析
(2)1
【分析】( 1 )连接 OE ,根据已知条件和切线的性质证明四边形 OFCE 是矩形,再根据矩形的性质证明 即可;
( 2 )根据题意,结合( 1 )可知 ,再由直角三角形中 “30° 角所对的直角边是斜边的一般 ” 的性质,可推导
,最后由
计算 AD 的长即可.
【详解】( 1 )解:如图,连接 OE ,
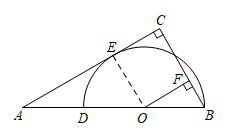
∵ AC 切半圆 O 于点 E ,
∴ OE ⊥ A C ,
∵ OF ⊥ BC , ,
∴∠ OEC = ∠ OFC = ∠ C = 90° .
∴ 四边形 OFCE 是矩形,
∴ OF = E C ;
( 2 ) ∵ ,
∴ ,
∵ , OE ⊥ AC ,
∴ ,
∴ .
【点睛】本题主要考查了切线的性质、矩形的判定与性质以及含 30° 角的直角三角形性质等知识,正确作出辅助线并灵活运用相关性质是解题关键.