如图，点 O 是 的边 AC 上一点，以点 O 为圆心， OA 为半径作 ，与 BC 相切于点 E ，交 AB 于点 D ，连接 OE ，连接 OD 并延长交 CB 的延长线于点 F ， ．

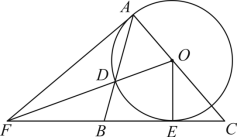
(1) 连接 AF ，求证： AF 是 的切线；

(2) 若 ， ，求 FD 的长．

答案

(1) 见解析

(2) FD 的长为

【分析】（ 1 ）根据 SAS 证 △ AOF ≌△ EOF ，得出 ∠ OAF ＝ ∠ OEF ＝ 90° ，即可得出结论；

（ 2 ）根据勾股定理求出 AF ，证 △ OEC ∽△ FAC ，设圆 O 的半径为 r ，根据线段比例关系列方程求出 r ，利用勾股定理求出 OF ，最后根据 FD ＝ OF ﹣ OD 求出即可．

（ 1 ）

证明：在 △ AOF 和 △ EOF 中，

，

∴△ AOF ≌△ EOF （ SAS ），

∴∠ OAF =∠ OEF ，

∵ BC 与 相切，

∴ OE ⊥ FC ，

∴∠ OAF =∠ OEF =90° ，

即 OA ⊥ AF ，

∵ OA 是 的半径，

∴ AF 是 的切线；

（ 2 ）

解：在 中， ∠ CAF =90° ， FC =10 ， AC =6 ，

∴ ，

∵ BC 与 相切， AF 是 的切线

∴∠ OEC ＝ ∠ FAC ＝ ∠90° ，

∵∠ OCE =∠ FCA ，

∴△ OEC ∽△ FAC ，

∴ ，

设 的半径为 r ，则 ，

解得 ，

在 Rt △ FAO 中， ∠ FAO =90° ， AF =8 ， ，

∴ ，

∴ ，

即 FD 的长为 ．

【点睛】本题主要考查切线的判定和性质、相似三角形的判定和性质、全等三角形的判定和性质、勾股定理等知识，熟练掌握切线的判定和性质是解题的关键．