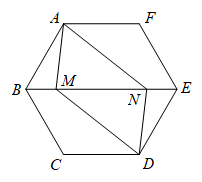
如图,在正六边形 中,
,
是对角线
上的两点,添加下列条件中的一个: ①
; ②
; ③
; ④
.能使四边形
是平行四边形的是 __________ (填上所有符合要求的条件的序号).
答案
①②④
【分析】根据正六边形的性质,依次结合题给的条件,先证有关三角形是否全等,再证四边形 是平行四边形.
【详解】解:由正六边形的性质知:
∠ ABM =∠ DEN , AB = DE , ∠ BAF =∠ CDE ,
① 若 BM = EN ,
在 △ ABM 和 △ DEN 中,
,
∴ ( SAS ),
∴ AM = DN , ∠ AMB =∠ DNE ,
∴∠ AMN =∠ DNM ,
∴ AM DN ,
∴ 四边形 是平行四边形;
② 若 ,则
∠ BAN =∠ EDM ,
在 和
中,
,
∴ (ASA) ,
∴ AN = DM , ∠ ANM =∠ DMN ,
∴ AN DM
∴ 四边形 是平行四边形;
③ 若 ,结合条件 AB = DE , ∠ ABM =∠ DEN , SSA 无法证明
,也就无法证明四边形
是平行四边形;
④ 若 ,
在 △ ABM 和 △ DEN 中,
,
∴ ( AAS ),
∴ AM = DN , ∠ AMB =∠ DNE ,
∴∠ AMN =∠ DNM ,
∴ AM DN ,
∴ 四边形 是平行四边形;
综上所述, ①②④ 符合题意.
故答案为: ①②④ .
【点睛】此题考查了正六边形的性质、全等三角形的判定以及平行四边形的判定.解题的关键是熟练运用上述知识逐一进行判断.