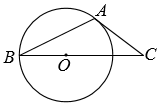
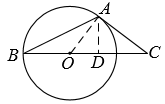
如图,在 △ ABC 中, AC =2 , BC =4 ,点 O 在 BC 上,以 OB 为半径的圆与 AC 相切于点 A , D 是 BC 边上的动点,当 △ ACD 为直角三角形时, AD 的长为 ___________ .
答案
或
【分析】根据切线的性质定理,勾股定理,直角三角形的等面积法解答即可.
【详解】解:连接 OA ,
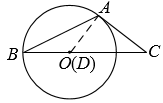
① 当 D 点与 O 点重合时, ∠ CAD 为 90° ,
设圆的半径 = r ,
∴ OA = r , OC =4- r ,
∵ AC =2 ,
在 Rt △ AOC 中,根据勾股定理可得: r 2 +4= ( 4- r ) 2 ,
解得: r = ,
即 AD = AO = ;
② 当 ∠ ADC =90° 时,过点 A 作 AD ⊥ BC 于点 D ,
∵ AO • AC =
OC • AD ,
∴ AD = ,
∵ AO = , AC =2 , OC =4- r =
,
∴ AD = ,
综上所述, AD 的长为 或
,
故答案为: 或
.
【点睛】本题主要考查了切线的性质和勾股定理,熟练掌握这些性质定理是解决本题的关键.

 。
。