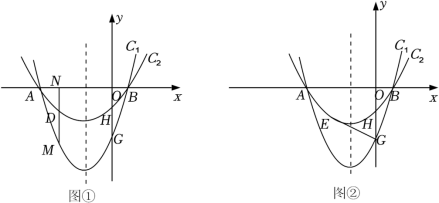
定义：由两条与 x 轴有着相同的交点，并且开口方向相同的抛物线所围成的封闭曲线称为 “ 月牙线 ” ，如图 ① ，抛物线 C ₁ ： y ＝ x ² +2 x ﹣ 3 与抛物线 C ₂ ： y ＝ ax ² +2 ax + c 组成一个开口向上的 “ 月牙线 ” ，抛物线 C ₁ 和抛物线 C ₂ 与 x 轴有着相同的交点 A （﹣ 3 ， 0 ）、 B （点 B 在点 A 右侧），与 y 轴的交点分别为 G 、 H （ 0 ，﹣ 1 ）．

(1) 求抛物线 C ₂ 的解析式和点 G 的坐标．

(2) 点 M 是 x 轴下方抛物线 C ₁ 上的点，过点 M 作 MN ⊥ x 轴于点 N ，交抛物线 C ₂ 于点 D ，求线段 MN 与线段 DM 的长度的比值．

(3) 如图 ② ，点 E 是点 H 关于抛物线对称轴的对称点，连接 EG ，在 x 轴上是否存在点 F ，使得 △ EFG 是以 EG 为腰的等腰三角形？若存在，请求出点 F 的坐标；若不存在，请说明理由．

答案

(1) y ＝ x ² + x ﹣ 1 ， G （ 0 ，﹣ 3 ）

(2)

(3) 存在，（ ﹣ 2 ， 0 ）或（﹣ ﹣ 2 ， 0 ）

【分析】（ 1 ）将 A （﹣ 3 ， 0 ）、 H （ 0 ，﹣ 1 ）代入 y ＝ ax ² +2 ax + c 中，即可求函数的解析式．

（ 2 ）设 M （ t ， t ² +2 t ﹣ 3 ），则 D （ t ， ）， N （ t ， 0 ），分别求出 MN ， DM ，再求比值即可．

（ 3 ）先求出 E （﹣ 2 ，﹣ 1 ），设 F （ x ， 0 ），分来两种情况讨论： ① 当 EG ＝ EF 时， ，可得 F （ ﹣ 2 ， 0 ）或（﹣ ﹣ 2 ， 0 ）； ② 当 EG ＝ FG 时， 2 ＝ ， F 点不存在．

【详解】（ 1 ）解：将 A （﹣ 3 ， 0 ）、 H （ 0 ，﹣ 1 ）代入 y ＝ ax ² +2 ax + c 中，

∴ ，

解得 ，

∴ y ＝ x ² + x ﹣ 1 ，

在 y ＝ x ² +2 x ﹣ 3 中，令 x ＝ 0 ，则 y ＝﹣ 3 ，

∴ G （ 0 ，﹣ 3 ）．

（ 2 ）设 M （ t ， t ² +2 t ﹣ 3 ），则 D （ t ， ）， N （ t ， 0 ），

∴ NM ＝﹣ t ² ﹣ 2 t +3 ， ，

∴ ＝ ．

（ 3 ）存在点 F ，使得 △ EFG 是以 EG 为腰的等腰三角形，理由如下：

由（ 1 ）可得 y ＝ x ² +2 x ﹣ 3 的对称轴为直线 x ＝﹣ 1 ，

∵ E 点与 H 点关于对称轴 x ＝﹣ 1 对称，

∴ E （﹣ 2 ，﹣ 1 ），

设 F （ x ， 0 ），

① 当 EG ＝ EF 时，

∵ G （ 0 ，﹣ 3 ），

∴ EG ＝ 2 ，

∴2 ＝ ，

解得 x ＝ ﹣ 2 或 x ＝﹣ ﹣ 2 ，

∴ F （ ﹣ 2 ， 0 ）或（﹣ ﹣ 2 ， 0 ）；

② 当 EG ＝ FG 时， 2 ＝ ，

此时 x 无解；

综上所述： F 点坐标为（ ﹣ 2 ， 0 ）或（﹣ ﹣ 2 ， 0 ）．

【点睛】本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，等腰三角形的性质，分类讨论是解题的关键．