如图，在 Rt△ ABC 中， ∠ B ＝ 90° ， AE 平分 ∠ BAC 交 BC 于点 E ， O 为 AC 上一点，经过点 A 、 E 的 ⊙ O 分别交 AB 、 AC 于点 D 、 F ，连接 OD 交 AE 于点 M ．

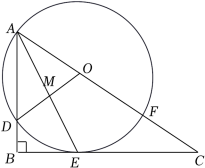
(1) 求证： BC 是 ⊙ O 的切线．

(2) 若 CF ＝ 2 ， sin C ＝ ，求 AE 的长．

答案

(1) 见解析

(2)

【分析】（ 1 ）连接 OE ，方法一：根据角平分线的性质及同弧所对的圆周角是圆心角的一半得出 ∠ OEC ＝ 90° 即可；

方法二：根据角平分线的性质和等腰三角形的性质得出 ∠ OEC ＝ 90° 即可；

（ 2 ）连接 EF ，根据三角函数求出 AB 和半径的长度，再利用三角函数求出 AE 的长即可．

【详解】（ 1 ）连接 OE ，

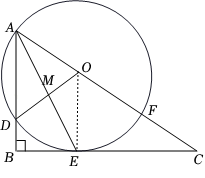
方法一： ∵ AE 平分 ∠ BAC 交 BC 于点 E ，

∴∠ BAC ＝ 2∠ OAE ，

∵∠ FOE ＝ 2∠ OAE ，

∴∠ FOE ＝ ∠ BAC ，

∴ OE ∥ AB ，

∵∠ B ＝ 90° ，

∴ OE ⊥ BC ，

又 ∵ OE 是 ⊙ O 的半径，

∴ BC 是 ⊙ O 的切线；

方法二： ∵ AE 平分 ∠ BAC 交 BC 于点 E ，

∴∠ OAE ＝ ∠ BAE ，

∵ OA ＝ OE ，

∴∠ OAE ＝ ∠ OEA ，

∴∠ BAE ＝ ∠ OEA ，

∴ OE ∥ AB ，

∵∠ B ＝ 90° ，

∴ OE ⊥ BC ，

又 ∵ OE 是 ⊙ O 的半径，

∴ BC 是 ⊙ O 的切线；

（ 2 ）连接 EF ，

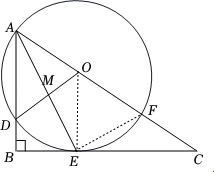
∵ CF ＝ 2 ， sin C ＝ ，

∴ ，

∵ OE ＝ OF ，

∴ OE ＝ OF ＝ 3 ，

∵ OA ＝ OF ＝ 3 ，

∴ AC ＝ OA + OF + CF ＝ 8 ，

∴ AB ＝ AC •sin C ＝ 8× ＝ ，

∵∠ OAE ＝ ∠ BAE ，

∴cos∠ OAE ＝ cos∠ BAE ，

即 ，

∴ ，

解得 AE ＝ （舍去负数），

∴ AE 的长为 ．

【点睛】本题主要考查切线的判定和三角函数的应用，熟练掌握切线的判定定理和三角函数是解题的关键．