已知二次函数 y ＝﹣ x ² +4 x +5 及一次函数 y ＝﹣ x + b ，将该二次函数在 x 轴上方的图象沿 x 轴翻折到 x 轴下方，图象的其余部分不变，得到一个新图象（如图所示），当直线 y ＝﹣ x + b 与新图象有 4 个交点时， b 的取值范围是 _____ ．

答案

【分析】解方程﹣ x ² +4 x +5 ＝ 0 得 A （﹣ 1 ， 0 ）， B （ 5 ， 0 ），再利用折叠的性质求出折叠部分的解析式为 ，即 y ＝ x ² ﹣ 4 x ﹣ 5 （﹣ 1≤ x ≤5 ），然后求出直线 y ＝﹣ x + b 经过点 A （﹣ 1 ， 0 ）时 b 的值和当直线 y ＝﹣ x + b 与抛物线 y ＝ x ² ﹣ 4 x ﹣ 5 （﹣ 1≤ x ≤5 ）有唯一公共点时 b 的值，从而得到当直线 y ＝﹣ x + b 与新图象有 4 个交点时， b 的取值范围．

【详解】解：如图所示：

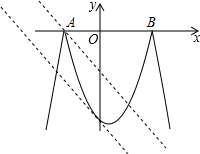
当 y ＝ 0 时，﹣ x ² +4 x +5 ＝ 0 ，解得 x ₁ ＝﹣ 1 ， x ₂ ＝ 5 ，则 A （﹣ 1 ， 0 ）， B （ 5 ， 0 ），

将该二次函数在 x 轴上方的图象沿 x 轴翻折到 x 轴下方的部分图象的解析式为 ，

即 y ＝ x ² ﹣ 4 x ﹣ 5 （﹣ 1≤ x ≤5 ），

当直线 y ＝﹣ x + b 经过点 A （﹣ 1 ， 0 ）时， 1+ b ＝ 0 ，解得 b ＝﹣ 1 ；

当直线 y ＝﹣ x + b 与抛物线 y ＝ x ² ﹣ 4 x ﹣ 5 （﹣ 1≤ x ≤5 ）有唯一公共点时，方程 ，即 有相等的实数解，即

解得 ，

所以当直线 y ＝﹣ x + b 与新图象有 4 个交点时， b 的取值范围为 ＜ b ＜﹣ 1 ，

故答案为： ．

【点睛】本题考查了抛物线与 x 轴的交点：把求二次函数 y ＝ ax ² + bx + c （ a ， b ， c 是常数， a ≠0 ）与 x 轴的交点坐标问题转化为解关于 x 的一元二次方程．也考查了二次函数图象与几何变换．