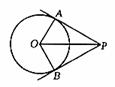
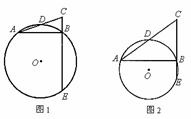
如图，四边形 内接于圆 ， 是直径，点 是 的中点，延长 交 的延长线于点 ．

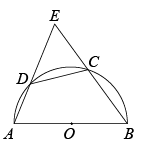
(1) 求证： ；

(2) 若 ， ，求 的长．

答案

(1) 见解析

(2)1

【分析】 （ 1 ）连接 ，根据圆周角推论得 ，根据 点 是 的中点得 ， ，用 ASA 证明 ，即可得；

（ 2 ）根据题意和全等三角形的性质得 ，根据四边形 ABCD 内接于圆 O 和角之间的关系得 ，即可得 ，根据相似三角形的性质得 ，即可得

【详解】（ 1 ） 证明：如图所示，连接 ，

为直径，

，

又 点 是 的中点

， ，

在 和 中，

，

，

；

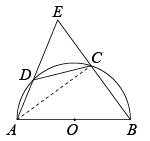
（ 2 ） 解： ， ，

，

又 四边形 内接于圆 ，

，

又 ，

，

又 ，

，

，

即： ，

解得： ，

．

【点睛】 本题考查相似三角形的判定和性质，全等三角形的判定和性质，圆周角定理，理解相关性质定理，正确添加辅助线是解题关键．