如图是由小正方形组成的 网格,每个小正方形的顶点叫做格点.
的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
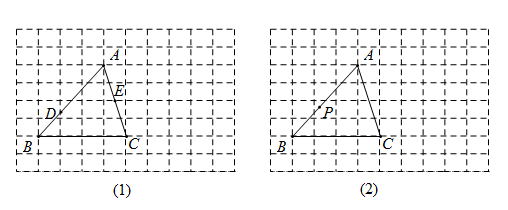
(1) 在图( 1 )中, ,
分别是边
,
与网格线的交点.先将点
绕点
旋转
得到点
,画出点
,再在
上画点
,使
;
(2) 在图( 2 )中, 是边
上一点,
.先将
绕点
逆时针旋转
,得到线段
,画出线段
,再画点
,使
,
两点关于直线
对称.
答案
(1) 作图见解析
(2) 作图见解析
【分析】( 1 )取格点,作平行四边形,利用平行四边形对角顶点关于对角线交点对称即可求点 F ;平行四边形对边在网格中与格线的交点等高,连接等高点即可作出 ;
( 2 )取格点,作垂直平分线即可作出线段 AH ;利用垂直平分线的性质,证明三角形全等,作出 ,
两点关于直线
对称
【详解】( 1 )解:作图如下:
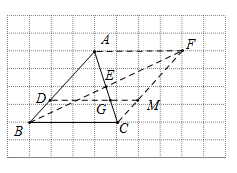
取格点 ,连接
,
且
,所以四边形
是平行四边形,连接
,与 AC 的交点就是点 E ,所以 BE = EF ,所以点 F 即为所求的点;
连接 CF ,交格线于点 M ,因为四边形 ABCF 是平行四边形,连接 DM 交 AC 于一点,该点就是所求的 G 点;
( 2 )解:作图如下:
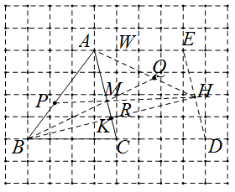
取格点 D 、 E ,连接 DE , AC 平行于 DE ,取格点 R ,连接 BR 并延长 BR 交 DE 于一点 H ,连接 AH ,此线段即为所求作线段;
理由如下:取格点 W 连接 AW 、 CW ,连接 CR ,
∴ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∵ 点 是
的中点,
∴ 点 是
的中点,
即 ,
∴ 垂直平分
,
∴ .
连接 ,交 AC 于点
,连接
交
于点
,则该点就是点
关于
直线的对称点.
理由如下: ∵ 垂直平分
,
∴ 是等腰三角形,
,
∴ ,
∴ ,
∴ ,
∴ ,
两点关于直线
对称 .
【点睛】本题考查了用无刻度直尺在网格中作图的知识,找准格点作出平行四边形和垂直平分线是解决本题的关键.