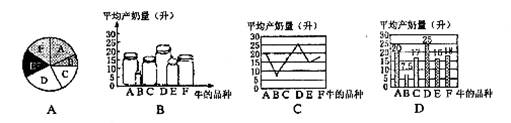
某工厂进行厂长选拔,从中抽出一部分人进行筛选,其中有 “ 优秀 ” , “ 良好 ” , “ 合格 ” , “ 不合格 ” .
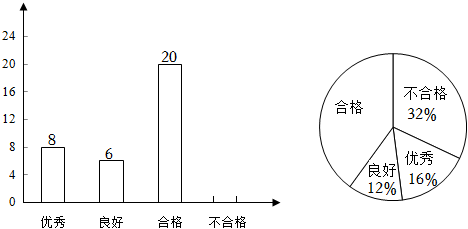
(1) 本次抽查总人数为 , “ 合格 ” 人数的百分比为 .
(2) 补全条形统计图.
(3) 扇形统计图中 “ 不合格人数 ” 的度数为 .
(4) 在 “ 优秀 ” 中有甲乙丙三人,现从中抽出两人,则刚好抽中甲乙两人的概率为 .
答案
(1)50 人, ;
(2) 见解析
(3)
(4)
【分析】( 1 )由优秀人数及其所占百分比可得总人数,根据百分比之和为 1 可得合格人数所占百分比;
( 2 )总人数乘以不合格人数所占百分比求出其人数,从而补全图形;
( 3 )用 乘以样本中 “ 不合格人数 ” 所占百分比即可得出答案;
( 4 )列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【详解】( 1 )解:本次抽查的总人数为 (人
,
“ 合格 ” 人数的百分比为 ,
故答案为: 50 人, ;
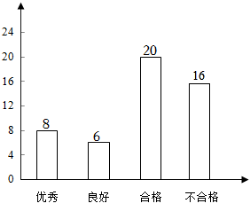
( 2 )解:不合格的人数为: ;
补全图形如下:
( 3 )解:扇形统计图中 “ 不合格 ” 人数的度数为 ,
故答案为: ;
( 4 )解:列表如下:
| | 甲 | 乙 | 丙 |
| 甲 | | (乙,甲) | (丙,甲) |
| 乙 | (甲,乙) | | (丙,乙) |
| 丙 | (甲,丙) | (乙,丙) | |
由表知,共有 6 种等可能结果,其中刚好抽中甲乙两人的有 2 种结果,
所以刚好抽中甲乙两人的概率为 .
故答案为: .
【点睛】本题考查了列表法或树状图法求概率、扇形统计图与条形统计图的关联,读懂统计图中的信息、画出树状图或列表是解题的关键.