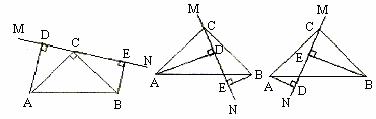
华师版八年级下册数学教材第 121 页习题 19.3 第 2 小题及参考答案.
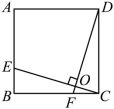
| 2 .如图,在正方形 ABCD 中, 证明:设 CE 与 DF 交于点 O , ∵ 四边形 ABCD 是正方形, ∴ ∴ ∵ ∴ ∴ ∴ ∴ ∴ |
某数学兴趣小组在完成了以上解答后,决定对该问题进一步探究
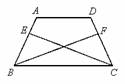
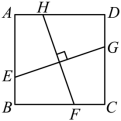
(1) 【问题探究】如图,在正方形 ABCD 中,点 E 、 F 、 G 、 H 分别在线段 AB 、 BC 、 CD 、 DA 上,且 .试猜想
的值,并证明你的猜想.
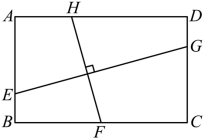
(2) 【知识迁移】如图,在矩形 ABCD 中, ,
,点 E 、 F 、 G 、 H 分别在线段 AB 、 BC 、 CD 、 DA 上,且
.则
______ .
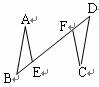
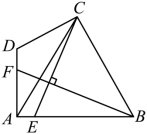
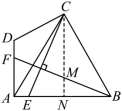
(3) 【拓展应用】如图,在四边形 ABCD 中, ,
,
,点 E 、 F 分别在线段 AB 、 AD 上,且
.求
的值.
答案
(1)1 ;证明见解析
(2)
(3)
【分析】( 1 )过点 A 作 AM ∥ HF 交 BC 于点 M ,作 AN ∥ EG 交 CD 的延长线于点 N ,利用正方形 ABCD , AB = AD , ∠ ABM = ∠ BAD = ∠ ADN = 90° 求证 △ ABM ≌△ ADN 即可.
( 2 )过点 A 作 AM ∥ HF 交 BC 于点 M ,作 AN ∥ EC 交 CD 的延长线于点 N ,利用在矩形 ABCD 中, BC = AD , ∠ ABM = ∠ BAD = ∠ ADN = 90° ,求证 △ ABM ∽△ ADN .再根据其对应边成比例,将已知数值代入即可.
( 3 )先证 是等边三角形,设
,过点
,垂足为
,交
于点
,则
,在
中,利用勾股定理求得
的长,然后证
,利用相似三角形的对应边对应成比例即可求解.
( 1 )
,理由为:
过点 A 作 AM ∥ HF 交 BC 于点 M ,作 AN ∥ EG 交 CD 的延长线于点 N ,
∵ 四边形 ABCD 是正方形,
∴ AB ∥ CD , AD ∥ BC ,
∴ 四边形 AMFH 是平行四边形,四边形 AEGN 是平行四边形,
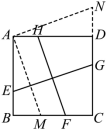
∴ AM = HF , AN = EG ,
在正方形 ABCD 中, AB = AD , ∠ ABM = ∠ BAD = ∠ ADN = 90°
∵ EG ⊥ FH ,
∴∠ NAM = 90° ,
∴∠ BAM = ∠ DAN ,
在 △ ABM 和 △ ADN 中, ∠ BAM = ∠ DAN , AB = AD , ∠ ABM = ∠ ADN
∴△ ABM ≌△ ADN
∴ AM = AN ,即 EG = FH ,
∴ ;
( 2 )
解:过点 A 作 AM ∥ HF 交 BC 于点 M ,作 AN ∥ EC 交 CD 的延长线于点 N ,
∵ 四边形 ABCD 是矩形,
∴ AB ∥ CD , AD ∥ BC ,
∴ 四边形 AMFH 是平行四边形,四边形 AEGN 是平行四边形,
∴ AM = HF , AN = EG ,
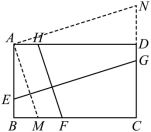
在矩形 ABCD 中, BC = AD , ∠ ABM = ∠ BAD = ∠ ADN = 90° ,
∵ EG ⊥ FH ,
∴∠ NAM = 90° ,
∴∠ BAM = ∠ DAN .
∴△ ABM ∽△ ADN ,
∴ ,
∵ ,
, AM = HF , AN = EG ,
∴ ,
∴ ;
故答案为:
( 3 )
解: ∵ ,
,
∴ 是等边三角形,
∴ 设 ,
过点 ,垂足为
,交
于点
,则
,
在 中,
,
∵ ,
,
∴ ,
,
又 ∵ ,
∴ ,
∵ ,
,
∴ ,
∴ ,
∴ ,即
.
【点睛】此题主要考查学生对相似三角形的判定与性质,全等三角形的判定与性质,勾股定理等知识点的理解和掌握,综合性较强,难度较大,是一道难题.