已知抛物线 与 x 轴交于 A ， B 两点（点 A 在点 B 的左侧）．

(1) 求点 A ，点 B 的坐标；

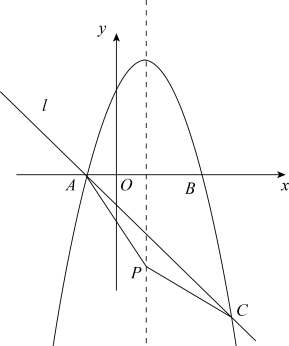
(2) 如图，过点 A 的直线 与抛物线的另一个交点为 C ，点 P 为抛物线对称轴上的一点，连接 ，设点 P 的纵坐标为 m ，当 时，求 m 的值；

(3) 将线段 AB 先向右平移 1 个单位长度，再向上平移 5 个单位长度，得到线段 MN ，若抛物线 与线段 MN 只有一个交点，请 直接写出 a 的取值范围．

答案

(1) A （ -1 ， 0 ）， B （ 3 ， 0 ）

(2)-3

(3) 或 或

【分析】（ 1 ）令 ，由抛物线解析式可得 ，解方程即可确定点 A ，点 B 的坐标；

（ 2 ）由抛物线解析式确定其对称轴为 ，可知点 P （ 1 ， m ），再将直线 l 与抛物线解析式联立，解方程组可确定点 C 坐标，由 列方程求解即可；

（ 3 ）根据题意先确定点 M （ 0 ， 5 ）、 N （ 4 ， 5 ）．可分 和 两种情况：当 时，抛物线的顶点大于或等于 5 ，把 代入， y 的值小于或等于 5 ，从而求得结果；当 时，将 代入抛物线解析式， y 的值大于或等于 5 ，从而求得结果．

【详解】（ 1 ）解：抛物线解析式 ，令 ，

可得 ，

解得 ， ，

故点 A 、 B 的坐标分别为 A （ -1 ， 0 ）， B （ 3 ， 0 ）；

（ 2 ）对于抛物线 ，其对称轴为 ，

∵ 点 P 为抛物线对称轴上的一点，且点 P 的纵坐标为 m ，

∴ P （ 1 ， m ），

将直线 l 与抛物线解析式联立，可得

，可解得 或 ，

故点 C 坐标为（ 4 ， -5 ），

∴ ，

，

当 时，可得 ，

解得 ；

（ 3 ）将线段 AB 先向右平移 1 个单位长度，再向上平移 5 个单位长度，得到线段 MN ，

结合（ 1 ），可知 M （ 0 ， 5 ）、 N （ 4 ， 5 ），

∵ ，

∴ 该抛物线的对称轴为 ，其顶点坐标为 ，

① 当 ，即 时，抛物线顶点在线段 MN 上，此时抛物线 与线段 MN 只有一个交点；

② 若抛物线顶点不在线段 MN 上，

当 时，如图 1 ，

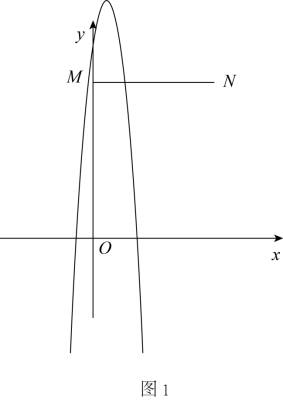
结合抛物线的对称性，可知若与线段 MN 只有一个交点，则抛物线的顶点大于 5 ，且 时， y 的值小于或等于 5 ， 时， y 的值大于 5 ，

即 ，

解得 ；

② 当 时，如图 2 ，

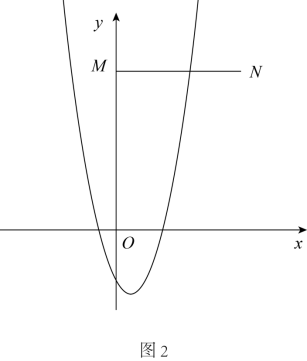
当 时， ，

若与线段 MN 只有一个交点，则当 时， y 的值大于或等于 5 ，

即 ，

解得 ；

综上所述，当抛物线 与线段 MN 只有一个交点时， a 的取值范围为 或 或 ．

【点睛】本题主要考查了二次函数的综合应用，包括求二次函数与 x 轴的交点、勾股定理的应用、利用二次函数解决图形问题等知识，解题关键是熟练运用数形结合和分类讨论的思想分析问题．