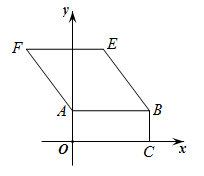
如图,在平面直角坐标系 xOy 中,矩形 OABC 的顶点 B 的坐标为 (10 , 4) ,四边形 ABEF 是菱形,且 tan∠ ABE = .若直线 l 把矩形 OABC 和菱形 ABEF 组成的图形的面积分成相等的两部分,则直线 l 的解析式为( )
A . B .
C . D .
答案
D
【分析】过点 E 作 EG ⊥ AB 于点 G ,利用三角函数求得 EG =8 , BG 6 , AG =4 ,再求得点 E 的坐标为 (4 , 12) ,根据题意,直线 l 经过矩形 OABC 的对角线的交点 H 和菱形 ABEF 的对角线的交点 D ,根据中点坐标公式以及待定系数法即可求解.
【详解】解:过点 E 作 EG ⊥ AB 于点 G ,
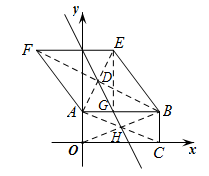
∵ 矩形 OABC 的顶点 B 的坐标为 (10 , 4) ,四边形 ABEF 是菱形,
∴ AB = BE =10 ,点 A 的坐标为 (0 , 4) ,点 C 的坐标为 (10 , 0) ,
在 Rt △ BEG 中, tan∠ ABE = , BE =10 ,
∴sin∠ ABE = ,即
,
∴ EG =8 , BG = 6 ,
∴ AG =4 ,
∴ 点 E 的坐标为 (4 , 12) ,
根据题意,直线 l 经过矩形 OABC 的对角线的交点 H 和菱形 ABEF 的对角线的交点 D ,
点 H 的坐标为 ( ,
) ,点 D 的坐标为 (
,
) ,
∴ 点 H 的坐标为 (5 , 2) ,点 D 的坐标为 (2 , 8) ,
设直线 l 的解析式为 y = kx + b ,
把 (5 , 2) , (2 , 8) 代入得 ,
解得: ,
∴ 直线 l 的解析式为 y =-2 x +12 ,
故选: D .
【点睛】本题考查了解直角三角形,待定系数法求函数的解析式,矩形和菱形的性质,解题的关键是灵活运用所学知识解决问题.