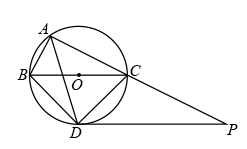
如图， 是 的外接圆，点 O 在 BC 上， 的角平分线交 于点 D ，连接 BD ， CD ，过点 D 作 BC 的平行线与 AC 的延长线相交于点 P ．

(1) 求证： PD 是 的切线；

(2) 求证： ∽ ；

(3) 若 ， ，求点 O 到 AD 的距离．

答案

(1) 见解析

(2) 见解析

(3) 点 O 到 AD 的距离为

【分析】（ 1 ）连接 OD ，证明 ，则 ，即可得证；

（ 2 ）由 ， ，可得 ，根据四边形 ABDC 为圆内接四边形，又 ，可得 ，即可证明 ∽ ；

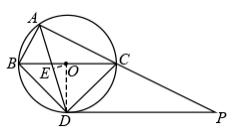
（ 3 ）过点 O 作 于点 E ，由 ∽ ，根据相似三角形的性质可求得 ，证明 ∽ ，继而求得 ，在 中，利用勾股定理即可求解．

（ 1 ）

证明：连接 OD ，

∵ AD 平分 ，

∴ ，

∴ ．

又 ∵ BC 为直径，

∴ O 为 BC 中点，

∴ ．

∵ ，

∴ ．

又 ∵ OD 为半径，

∴ PD 是 的切线；

（ 2 ）

证明： ∵ ，

∴ ．

∵ ，

∴ ．

∵ 四边形 ABDC 为圆内接四边形，

∴ ．

又 ∵ ，

∴ ，

∴ ∽ ．

（ 3 ）

过点 O 作 于点 E ，

∵ BC 为直径，

∴ ．

∵ ， ，

∴ ．

又 ∵ ，

∴ ，

∴ ．

由（ 2 ）知 ∽ ，

∴ ，

∴ ，

∴ ．

又 ∵ ， ，

∴ ∽ ，

∴ ，

∴ ，

∴ ．

∵ ，

∴ ．

在 中， ，

∴ 点 O 到 AD 的距离为 ．

【点睛】本题考查了切线的性质与判定，圆内接四边形对角互补，相似三角形的性质与判定，勾股定理，掌握以上知识是解题的关键．