如图， △ ABC 内接于 ⊙ O ， AB 是 ⊙ O 的直径， ⊙ O 的切线 PC 交 BA 的延长线于点 P ， OF ∥ BC 交 AC 于点 E ，交 PC 于点 F ，连接 AF ．

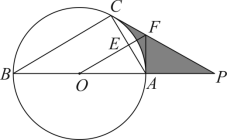
(1) 判断直线 AF 与 ⊙ O 的位置关系并说明理由；

(2) 若 ⊙ O 的半径为 6 ， AF ＝ 2 ，求 AC 的长；

(3) 在（ 2 ）的条件下，求阴影部分的面积．

答案

(1) 直线 AF 与 ⊙ O 相切．理由见解析

(2)6

(3)18 ﹣ 6π ．

【分析】（ 1 ）连接 OC ，证明 △ AOF ≌△ COF （ SAS ），由全等三角形的判定与性质得出 ∠ OAF =∠ OCF =90° ，由切线的判定可得出结论；

（ 2 ）由直角三角形的性质求出 ∠ AOF =30° ，可得出 AE = OA =3 ，则可求出答案；

（ 3 ）证明 △ AOC 是等边三角形，求出 ∠ AOC =60° ， OC =6 ，由三角形面积公式和扇形的面积公式可得出答案．

【详解】（ 1 ）直线 AF 与 ⊙ O 相切．

理由如下：连接 OC ，

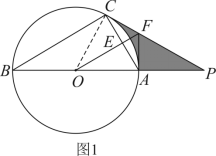
∵ PC 为圆 O 切线，

∴ CP ⊥ OC ，

∴∠ OCP ＝ 90° ，

∵ OF ∥ BC ，

∴∠ AOF ＝ ∠ B ， ∠ COF ＝ ∠ OCB ，

∵ OC ＝ OB ，

∴∠ OCB ＝ ∠ B ，

∴∠ AOF ＝ ∠ COF ，

∵ 在 △ AOF 和 △ COF 中，

，

∴△ AOF ≌△ COF （ SAS ），

∴∠ OAF ＝ ∠ OCF ＝ 90° ，

∴ AF ⊥ OA ，

又 ∵ OA 为圆 O 的半径，

∴ AF 为圆 O 的切线；

（ 2 ） ∵△ AOF ≌△ COF ，

∴∠ AOF ＝ ∠ COF ，

∵ OA ＝ OC ，

∴ E 为 AC 中点，

即 ，

∵∠ ，

∴ ，

∴∠ AOF ＝ 30° ，

∴ ，

∴ ；

（ 3 ） ∵ AC ＝ OA ＝ 6 ， OC ＝ OA ，

∴△ AOC 是等边三角形，

∴∠ AOC ＝ 60° ， OC ＝ 6 ，

∵∠ OCP ＝ 90° ，

∴ ，

∴ S _△ OCP ＝ ，

∴ 阴影部分的面积 = S _△ OCP ﹣ S _扇形 AOC ＝ ．

【点睛】此题考查了切线的判定与性质，全等三角形的判定与性质，平行线的性质，等腰三角形的性质，解直角三角形，三角形的面积求法，等边三角形的判定与性质，扇形的面积公式，熟练掌握切线的判定与性质是解本题的关键．