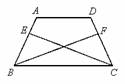
某校一数学兴趣小组在一次合作探究活动中，将两块大小不同的等腰直角三角形 和等腰直角三角形 ，按如图 1 的方式摆放， ，随后保持 不动，将 绕点 C 按逆时针方向旋转 （ ），连接 ， ，延长 交 于点 F ，连接 ．该数学兴趣小组进行如下探究，请你帮忙解答：

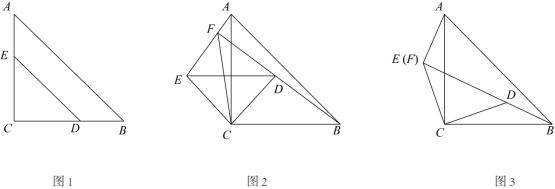
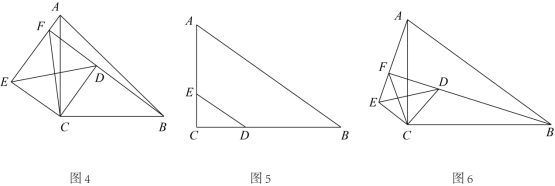
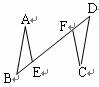
(1) 【初步探究】如图 2 ，当 时，则 _____ ；

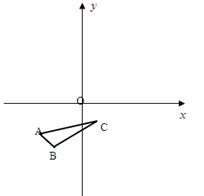
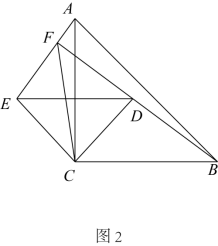
(2) 【初步探究】如图 3 ，当点 E ， F 重合时，请直接写出 ， ， 之间的数量关系： _________ ；

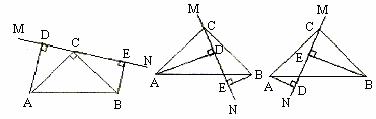
(3) 【深入探究】如图 4 ，当点 E ， F 不重合时，（ 2 ）中的结论是否仍然成立？若成立，请给出推理过程；若不成立，请说明理由．

(4) 【拓展延伸】如图 5 ，在 与 中， ，若 ， （ m 为常数）．保持 不动，将 绕点 C 按逆时针方向旋转 （ ），连接 ， ，延长 交 于点 F ，连接 ，如图 6 ．试探究 ， ， 之间的数量关系，并说明理由．

答案

(1)

(2)

(3) 仍然成立，理由见解析

(4)

【分析】（ 1 ）根据等腰直角三角形的性质，可得 ，根据题意可得 ，根据等原三角形的性质可得 平分 ，即可得 ，根据旋转的性质可知 ；

（ 2 ）证明 ，可得 ，根据等腰直角三角形可得 ，由 ，即可即可得出 ；

（ 3 ）同（ 2 ）可得 ，过点 ，作 ，交 于点 ，证明 ， ，可得 ，即可得出 ；

（ 4 ）过点 作 ，交 于点 ，证明 ，可得 ， ，在 中，勾股定理可得 ，即可得出 ．

【详解】（ 1 ） 等腰直角三角形 和等腰直角三角形 ，

，

故答案为：

（ 2 ）

在 与 中，

又

重合，

故答案为：

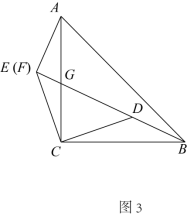
（ 3 ）同（ 2 ）可得

，

过点 ，作 ，交 于点 ，

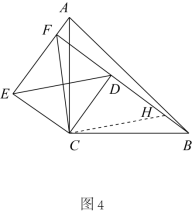
则 ，

，

在 与 中，

，

，

，

是等腰直角三角形，

， ，

，

，

在 与 中，

，

，

，

，

即 ，

（ 4 ）过点 作 ，交 于点 ，

， ，

，

，

，

，

，

，

，

，

，

， ，

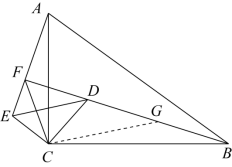
中， ，

，

即 ．

【点睛】本题考查了等腰直角三角形的性质，旋转的性质，全等三角形的性质与判定，相似三角形的性质与判定，掌握全等三角形的性质与判定，相似三角形的性质与判定是解题的关键．