如图 1 ，在矩形 中， ， ， 是 边上的一点，连接 ，将矩形 沿 折叠，顶点 恰好落在 边上的点 处，延长 交 的延长线于点 ．

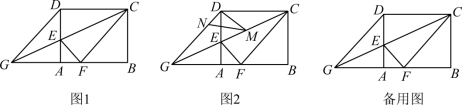
(1) 求线段 的长；

(2) 求证四边形 为菱形；

(3) 如图 2 ， ， 分别是线段 ， 上的动点（与端点不重合），且 ，设 ，是否存在这样的点 ，使 是直角三角形？若存在，请求出 的值；若不存在，请说明理由．

答案

(1)

(2) 见解析

(3) 存在， 或

【分析】（ 1 ）根据在 中， ，根据矩形的折叠与勾股定理即可求解；

（ 2 ）根据（ 1 ）的结论分别求得 ，根据四边相等的四边形是菱形即可得证；

（ 3 ）分 和 两种情况分别讨论即可求解．

（ 1 ）

解：如图

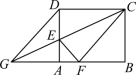
四边形 是矩形， ， ，

， ，

将矩形 沿 折叠，顶点 恰好落在 边上的点 处，

，

在 中， ，

，

设 ，则 ，

在 中， ，

，

解得 ，

；

（ 2 ）

，

，

四边形 是矩形，

，

，

，

，

，

中， ，

，

，

四边形 为菱形；

（ 3 ）

，设 ， 是直角三角形

设

由（ 2 ）可得

① 当 时，如图，

， ,

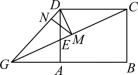
解得 ；

② 当 时，

同理可得

综上所述， 或

【点睛】本题考查了矩形的性质，折叠的性质，勾股定理，解直角三角形，菱形的判定，掌握以上知识是解题的关键．