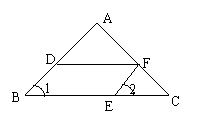
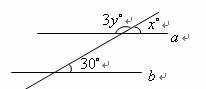
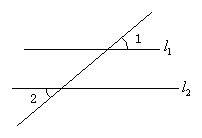
如图, ,将一个等腰直角三角板放置到如图所示位置.若
,则
的大小是( )
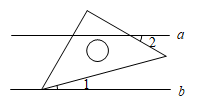
A . B .
C .
D .
答案
C
【分析】如图,过等腰直角三角板的一个顶点作直线 ,根据平行线的性质,可得
,根据三角板可知
,进而等量代换结合已知条件即可求解.
【详解】解:如图,过等腰直角三角板的一个顶点作直线
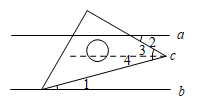
∵ a ∥ b ,
,
,
,
,
,
.
故选: C .
【点睛】本题考查了平行线的性质与判定,掌握平行线的性质是解题的关键.