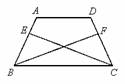
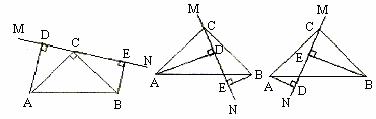
如图 1 ,在正方形 ABCD 中, E , F 分别是 BC , CD 边上的点(点 E 不与点 B , C 重合),且 .
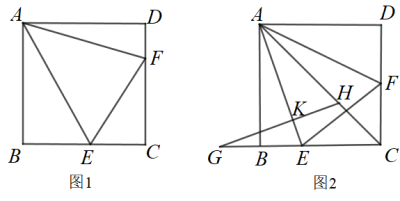
(1) 当 时,求证:
;
(2) 猜想 BE , EF , DF 三条线段之间存在的数量关系,并证明你的结论;
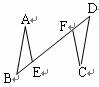
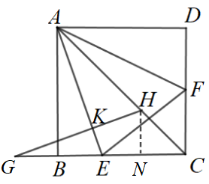
(3) 如图 2 ,连接 AC , G 是 CB 延长线上一点, ,垂足为 K ,交 AC 于点 H 且
.若
,
,请用含 a , b 的代数式表示 EF 的长.
答案
(1) 见解析
(2) ,见解析
(3)
【分析】( 1 )先利用正方表的性质求得 ,
,再利用判定三角形全等的 “SAS” 求得三角形全等,然后由全等三角形的性质求解;
( 2 )延长 CB 至 M ,使 ,连接 AM ,先易得
,推出
,
,进而得到
,最后利用全等三角形的性质求解;
( 3 )过点 H 作 于点 N ,易得
,进而求出
,再根据( 2 )的结论求解.
( 1 )
证明: ∵ 四边形 ABCD 是正方形,
∴ ,
.
在 和
中
,
∴ ,
∴ ;
( 2 )
解 : BE , EF , DF 存在的数量关系为 .
理由如下:
延长 CB 至 M ,使 ,连接 AM ,
则 .
在 和
中
,
∴ ,
∴ ,
.
∵ ,
∴ .
∴∠ MAE =∠ FAE ,
在 和
中
,
∴ ,
∴ EM = EF ,
∵ EM = BE + BM ,
∴ ;
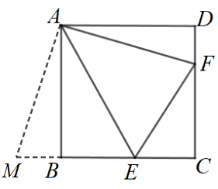
( 3 )
解:过点 H 作 于点 N ,
则 .
∵ ,
∴ ,
∴ .
在 和
中
,
∴ ,
∴ .
∵ ,
,
∴ ,
∴ ,
由( 2 )知, .
【点睛】本题主要考查了正方形的性质,全等三角形的判定和性质,特殊角的三角函数值,作出辅助线,构建三角形全等是解答关键.