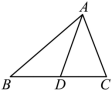
如图,在 △ ABC 中, AD 是 BC 边上的中线, AB = 6 , AD = 4 .则 BC 边的取值范围是 _________ .
答案
4< BC <20
【分析】在 △ ABD 中,利用据三角形三边关系求得 BD 的取值范围,据此即可求得 BC 边的取值范围.
【详解】解:在 △ ABD 中, AB = 6 , AD = 4 .
∴6-4< BD <6+4 ,即 2< BD <10 ,
∵ AD 是 BC 边上的中线,
∴ BC =2 BD ,
∴4< BC <20 ,
∴ BC 边的取值范围为 4< BC <20 ,
故答案为: 4< BC <20 .
【点睛】本题考查了三角形的三边关系,掌握三角形三边关系定理是解题的关键.