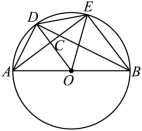
如图所示， AB 是 ⊙ O 的直径， AD = DE ， AE 与 BD 交于点 C ，则图中与 ∠ BCE 相等的角除对顶角外还有（ ）

A ． 2 个 B ． 3 个 C ． 4 个 D ． 5 个

答案

C

【分析】首先与 ∠ BCE 相等的角有对顶角 ∠ DCA ．由于 AB 是 ⊙ O 的直径，可得 ∠ ADB =90° ；已知 AD = DE ，证明 △ OAD ≌△ OED ，因此 ∠ DAB =∠ ADO =∠ ODE =∠ DEO ；由 AD = DE 得出 ，得出 ∠ ABD =∠ DBE ，得出 ∠ DAB =∠ BCE ，因此与 ∠ BCE 相等的角有 5 个： ∠ DCA 、 ∠ OAD 、 ∠ ODA 、 ∠ ODE 、 ∠ OED ．

【详解】解： ∵ 在 △ ADO 和 △ DOE 中

，

∴△ OAD ≌△ ODE （ SSS ），

∴∠ DAB =∠ EDO ， ∠ ADO =∠ DEO ，

∵ AO = DO ，

∴∠ DAB =∠ ADO ，

∴∠ DAB =∠ ADO =∠ ODE =∠ DEO ；

∵ AB 是 ⊙ O 的直径，

∴∠ ADB =90° ， ∠ AEB =90° ，

∵ AD = DE ，

∴ ，

∴∠ ABD =∠ DBE ，

∴∠ DAB =90°-∠ ABD ， ∠ BCE =90°-∠ DBE ，

∴∠ DAB =∠ BCE ，

∴∠ DCA =∠ DAB =∠ ADO =∠ ODE =∠ DEO ，

则与 ∠ ECB 相等的角有 5 个．

图中与 ∠ BCE 相等的角除对顶角外还有 4 个

故选 C ．

【点睛】此题主要考查圆周角定理，以及等腰三角形的性质，关键是掌握同弧所对的圆周角相等．