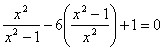我们已经学习了利用配方法解一元二次方程，其实配方法还有其他重要应用．

例：已知 可取任何实数，试求二次三项式 最小值．

解：

无论 取何实数，总有 ．

，即 的最小值是 ．

即无论 取何实数， 的值总是不小于 的实数．

问题：

（ 1 ）已知 ，求证 是正数．

知识迁移：

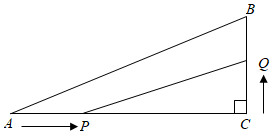
（ 2 ）如图，在 中， ， ， ，点 在边 上，从点 向点 以 的速度移动，点 在 边上以 的速度从点 向点 移动．若点 ， 同时出发，且当一点移动到终点时，另一点也随之停止，设 的面积为 ，运动时间为 秒，求 的最大值．

答案

（ 1 ）见解析 ; （ 2 ）当 时， 有最大值

【分析】（ 1 ）根据题意对 进行配方，即可求出最值；

（ 2 ）先求 ，再根据题意进行配方即可求得最值．

【详解】（ 1 ）证明：

．

．

．

．

是正数．

（ 2 ）解：由题意得： ， ， ．

．

．

．

又 ∵

当 时， 有最大值 ．

【点睛】本题考查利用配方法求最值，正确进行配方是求解本题的关键．