在 的方格内选 5 个小正方形．

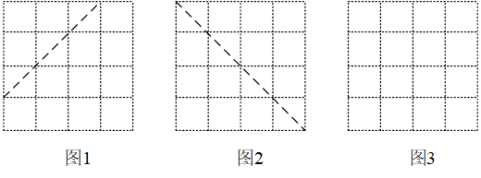
(1) 在图 1 中，让它们以虚线为对称轴，组成一个轴对称图形；在图 2 中，让它们以虚线为对称轴组成一个轴对称图形；在图 3 中，让它们构成一个中心对称图形．请在图中画出你的这 3 种方案．（每个 的方格内限画一种）

要求： ①5 个小正方形必须相连在一起（有公共边或公共顶点视为相连）； ② 将选中的小正方形方格用黑色签字笔涂成阴影图形．（若两个方案的图形能够重合，视为一种方案）

(2) 在你所画得三个图中，最喜欢的是哪一个？简要说明理由．

答案

(1) 见解析

(2) 见解析

【分析】（ 1 ）根据要求作出图形即可；

（ 2 ）根据自己的喜好判断即可．

（ 1 ）

解：如图所示，

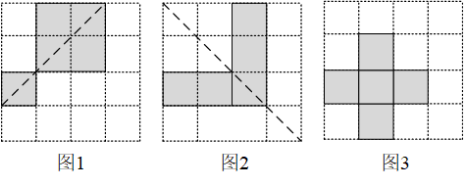
（ 2 ）

我更喜欢图 3 ，理由：它既是轴对称图形，也是中心对称图形（答案不唯一）．

【点睛】本题考查图案设计，中心对称图形，轴对称图形等知识，解题的关键是理解中心对称图形，轴对称图形的定义，属于中考常考题型．