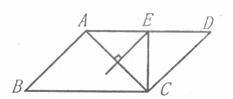
将一张矩形纸片 ABCD 按下图所示操作： ① 将 DA 沿 DP 向内折叠，使点 A 落在点 A ₁ 处． ② 将 DP 沿 DA ₁ 向内继续折叠，使点 P 落在点 P ₁ 处，折痕与边 AB 交于点 M ． 若 P ₁ M ⊥ AB ，则 ∠ DP ₁ M 的大小是（ ）

A ． 135° B ． 120° C ． 112.5° D ． 115°

答案

C

【分析】由折叠的性质可知 ∠ P ₁ M A ₁ =∠ PM A ₁ ， P P ₁ ⊥ DM ；进而求出 ∠ M P ₁ A ₁ 的度数，再根据 ∠ M P ₁ A ₁ 的度数求出 ∠ DP A 和 ∠D P A ₁ 的度数；最后根据折叠的性质求出答案即可．

【详解】 ∵ P ₁ M ⊥ AB ，

∴∠ P ₁ MP =90° ，

连接 PP ₁ ，

由折叠的性质可知， ∠ P ₁ M A ₁ =∠ PM A ₁ =45° ， PP ₁ ⊥ DM ，

∴ PP ₁ 经过点 A ₁ ，

∴∠ M P ₁ A ₁ =∠ BPA ₁ =45° ，

∴∠ APA ₁ =180°-45°=135° ，

由折叠的性质可知： ∠ DP A = ∠DPA ₁ =67.5° ，

∴∠ DPB = ∠D P A ₁ +∠ B P A ₁ =45°+67.5°=112.5° ，

由折叠的性质可知： ∠ DP ₁ M= ∠ DPB =112.5° ；

故选： C

【点睛】本题主要考查了折叠的性质，熟练地掌握经过折叠会形成轴对称图形，对应角度相等，对应点连线垂直于对称轴是解题的关键．