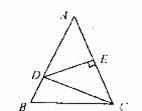
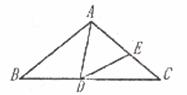
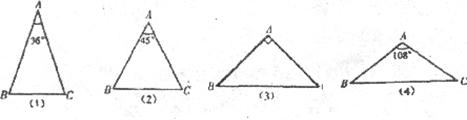
在如图所示的 纸片中， ， D 是斜边 AB 的中点，把纸片沿着 CD 折叠，点 B 到点 E 的位置，连接 AE ．若 ， ，则 等于（ ）

A ． B ． C ． D ．

答案

B

【分析】根据直角三角形斜边上的中线等于斜边的一半，可知 CD = BD = AD ，根据折叠的性质可知 ∠ B =∠ DCB =∠ DCE =∠ EDC = ，根据平行线的性质，可得出 ∠ AED =∠ EDC ，根据等边对等角即可求得 ∠ EAD 的度数，最后 =∠ EAD -∠ CAD 即可求出．

【详解】 ∵ D 是斜边 AB 的中点， △ ABC 为直角三角形，

∴ CD = BD = AD ，

∵△ CDE 由 △ CDB 沿 CD 折叠得到，

∴△ CDE ≌△ CDB ，

则 CD = BD = AD = ED ，

∴∠ B =∠ DCB =∠ DCE =∠ DEC = ，

∴∠ EDC =180°-2 ，

∵ ，

∴∠ AED =∠ EDC =180°-2 ，

∵ ED = AD ，

∴∠ EAD =∠ AED =180°-2 ，

∵∠ B = ， △ ABC 为直角三角形，

∴∠ CAD =90°- ，

∴ =∠ EAD -∠ CAD =180°-2 - （ 90°- ） =90°- ，

故选： B ．

【点睛】本题主要考查了直角三角形斜边上的中线等于斜边的一半，折叠的性质，等腰三角形的性质以及直角三角形两个锐角互余，熟练地掌握相关知识是解题的关键．