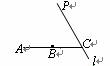
如图，将 △ ABC 沿 DE 、 EF 翻折，顶点 A 、 B 均落在点 O 处，且 EA 与 EB 重合于线段 EO ，若 ∠ C ＝ α ，则下列结论错误的是（ ）

A ． ∠ DOF ＝ 180° － α B ． AO EF

C ． AO ⊥ BO D ． ∠ ODE ＝ ∠ OED

答案

D

【分析】利用折叠的性质，找出对应边、对应角，结合三角形内角和定理、平行线的判定、垂直的定义逐项判断即可得出答案．

【详解】解：由折叠的性质可知， ， ，

∴ ，

∴∠ DOF ＝ 180° － α ．故 A 选项正确，不合题意；

由折叠的性质可知， ， ，

∴ ，

∴ ，

∴ ，

∵△ ABC 沿 DE 翻折，顶点 A 落在点 O 处，

∴ ，

∴ AO EF ．故 B 选项正确，不合题意；

由折叠的性质可知， ， ，

∴ ， ，

又 ∵ ，

∴ ，

∴ ．故 C 选项正确，不合题意；

∵ AD 不一定等于 AE ，

∴ OD 不一定等于 OE ，

∴ 不能判定 ∠ ODE ＝ ∠ OED ．故 D 选项错误，符合题意；

故选 D ．

【点睛】本题考查折叠的性质、三角形内角和定理、平行线的判定等知识，解题的关键是熟练掌握折叠的性质： 1 、折叠前后两个图形全等，对应边相等，对应角相等； 2 、对应点连线被对称轴垂直平分．